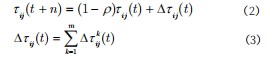SCI论文(www.lunwensci.com):
摘要:以TSP问题为背景研究基于蚁群算法的路径规划仿真技术。介绍了蚁群算法的基本原理,针对蚁周、蚁量、蚁密三种模型对蚁群算法进行仿真实现,实验不同启发式参数设置对算法效果的影响,讨论蚁群算法的改进策略。实验结果表明,蚁周模型具有更强的全局搜索能力,通过优化组合启发式参数,可以获得更好的算法改进。
关键词:蚁群算法;路径规划仿真;TSP;蚁周模型;启发式参数
Research of Path Planning Simulation Based on Ant Colony Algorithm
YANG Yang
(Hubei Polytechnic Institute School of Information Engineering,Xiaogan Hubei 432100)
【Abstract】:Study the ant colony algorithm of path planning simulation technology based on TSP problem.Introduce the basic principle of ant colony algorithm,realizing the simulation of ant colony algorithm on three different models:Ant-cycle,ant-quantity and ant-density,doing experiments to find the influence of different heuristic parameter settings on the algorithm,and giving the improved strategy of ant colony algorithm.Experimental results show that ant cycle model has stronger global search ability,and better algorithm improvement can be obtained by optimizing the combination of heuristic parameters.
【Key words】:ant colony algorithm;path planning simulation;TSP;ant-cycle model;ueuristic parameters
0引言
路径规划在日常生活生产中有广泛而重要的应用,包括智能机器人寻路和避障[1]、物流车辆规划[2]、无人飞行器航迹规划[3]、网络路由[4]等领域。在这些场景应用中,一个基本的要求就是从出发点到终点找到最快、最短路径。更加复杂的要求还包括避开静态、动态障碍物、寻找约束条件下的最优路径解、路径平滑[5]等。在不同的行业背景下,路径规划问题已经有较为成熟的解决方案,经典方法包括粒子群算法[6]、A*算法、蚁群算法、遗传算法[7]等启发式搜索法,也有基于人工智能的搜索算法[8]。本文以TSP问题为研究背景,研究讨论基于蚁群算法的路径规划仿真。
1蚁群算法
蚁群算法是模拟群体蚂蚁觅食过程的一种仿生算法。蚂蚁在行进过程中,会释放一种叫做“信息素”的化学物质,该物质能够吸引其他蚂蚁前来觅食。一般说来,发现食物的路径上积累的信息素越来越多,会生成一条从出发点到终点的最优路径。蚁群算法被广泛应用于各种优化问题,包括TSP问题、车辆路径选择等问题[9]。在这些问题中,通过不断朝着“信息素累积浓度多”的方向移动,并将该选择作为正反馈加强方向,使蚂蚁行进的最多路径被选择出来,从而在解空间中寻找到最优可行解。
基本的蚁群算法主要包括两个过程,即状态转移过程和信息素更新过程。第一阶段,当从一个节点选择转移到哪一个节点时,蚂蚁会根据节点之间的距离以及节点的信息素浓度来具体判断。第二阶段,当路过一个节点后,蚂蚁会释放相应量的信息素(与所行走的路径长度相关),从而更新节点的信息素量。假设当前问题域中有N个节点,M只蚂蚁,那么某一只蚂蚁k从节点i到节点j的转移概率[10]可以表示为如公式(1)所示:

其中,τij(t)表示时刻t,从节点i到节点j上的信息素的浓度;ηij(t)表示时刻t节点i到节点j上的能见度,它是节点i、j之间的距离倒数,即ηij(t)=1/dij;α、β是两个常数,属于启发式因子。allowed(k)表示蚂蚁k可以访问的节点集合。
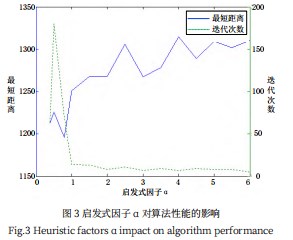
为了更真实模拟蚁群觅食过程,引入了信息素挥发因子ρ,表示信息素会随着时间而挥发,1-ρ表示信息素残留因子,那么t+n时刻节点i到节点j上的信息素浓度可表示为如公式(2)、公式(3)所示:
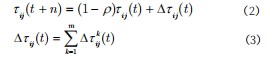
如公式(2)和公式(3)所示,t+n时刻节点i到节点j上的信息素浓度τij(t+n),既包括挥发后所余下的信息素(1-ρ)τij(t),也包括m只蚂蚁在节点i和节点j之间所累积释放的信息素之和∆τij(t)。通过引入信息素挥发因子ρ,可以避免公式(1)中因信息素积累过多,导致信息素积累量成为计算的决定因素,从而使蚂蚁在转移时总是偏向某些路径而忽略了其他潜在路径;也能够对启发信息过多而进入局部最优这种情况进行抑制调整,从而增强算法的整体适应能力和全局寻优能力。
基于公式(2)和公式(3),蚁群算法中∆τij(t)有三种计算方式[11],分别是蚁周模型(Ant-Cycle),当蚂蚁完成一次周游后再增加所走路径每条边上的信息素浓度Q/Lk;蚁量模型(Ant-Quantity),每走完一步即增加边ij浓度为Q/dij;蚁密模型(Ant-Density),每走完一步即增加边ij浓度为Q。其中,Lk表示第k只蚂蚁本次周游中走过的路径长度;Q是一个正常数,表示信息素强度,可调节算法的收敛速度;dij表示边ij的长度。
2蚁群算法实现
2.1 TSP问题
TSP问题[12],即旅行商问题(Traveling Salesman Problem),是一个经典的组合优化问题,它要求旅行商在N个城市之间找到一条最短路径,周游N个城市,不允许重复访问,并最终回到原点。TSP问题的研究广泛应用于芯片设计、电路板印制、路径规划等,在工业生产、交通运输等领域发挥重要作用。
2.2蚁群算法基本流程
针对TSP问题,根据蚁周模型、蚁量模型、蚁密模型的定义,其算法伪代码可以如表示1所示。三种模型基本框架相同,都是首先指定总迭代次数。在每一次迭代中,所有蚂蚁从随机起点开始进行“旅行商环游”,每一次选择下一个节点都是基于节点间的信息素浓度公式。三种模型所不同的是更新节点间信息素的时机和大小。蚁周模型在所有蚂蚁完成一次环游后整体更新,蚁量模型和蚁密模型在每前进一步后局部更新。
2.3蚁群算法实现
在算法实验中,随机生成50个城市的坐标,选择50只蚂蚁,最大迭代次数200次,分别采用蚁周模型、蚁量模型、蚁密模型编写程序,可得到如图1所示结果。结果表明,随着迭代次数的增加,蚁周模型的最短路径和平均距离呈逐步下降趋势,且收敛时可以获得更小的路径值,说明它可以更准确地找到最短路径。相比于蚁量模型和蚁密模型,蚁周模型选择在所有蚂蚁周游一次结束后更新信息素,且更新大小与周游一次的路径长度相关,从而具有更强的全局启发性。
2.4蚁群算法参数分析
蚁群算法包含多个参数,如公式(1)中的常数α、β,公式(2)中的信息素挥发因子ρ等,这些参数的设置影响了算法效率和最终生成结果。为了结合实际问题获得一个优化的参数组合,以TSP问题为实验背景,采用蚁周模型算法进行相关参数分析。
2.4.1信息素挥发因子ρ
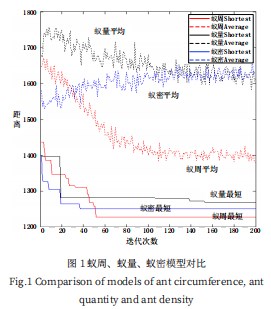
信息素挥发因子ρ表明路径上信息素的挥发程度,取值范围在0-1之间。如果ρ值较小,信息素在一定时间范围内挥发较慢,易产生信息素积聚在某些局部路径上,导致这些路径被后续的蚂蚁反复选中,减弱了蚁群算法的全局搜索能力,从而只能找到一种局部最优解;如果ρ值较大,表明信息素挥发较快,起不到信息素引导蚂蚁进行路径选择的作用,蚂蚁之间相互协调的功能大大降低,在算法中蚂蚁只能依靠节点间的距离及随机寻径策略做出判断,增加了算法迭代时间。为此需要找到全局最优解和迭代速度的折中ρ值。基于以上分析,设计如下实验:随机生成50个城市的坐标,蚂蚁的数量为50只,α=1,β=5,迭代次数IMax=200,ρ的取值范围为[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]。测试结果如图2所示,ρ值取0.1~0.9时,当最短距离值偏小(蓝色实线),迭代次数偏大(绿色虚线);收敛时迭代次数小,却最短距离值偏大。根据多次测试与观察,ρ的最佳取值范围在[0.4,0.6]之间,这个时候可以达到搜索质量与速度的平衡。
2.4.2启发式因子α
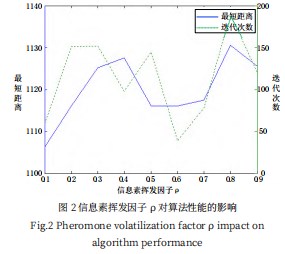
启发式因子α在公式(1)中对信息素浓度有强化的作用,反映了信息素浓度在路径选择中的重要程度。如果α值较小,信息素浓度的大小不能起到判定作用,蚂蚁间的信息传递减弱,不利于找到全局最优解,算法运行时间也因无序搜索而增长;如果α值较大,偏向选择信息素浓度高的节点,增加了算法搜索的确定性,但易生成局部最优解值。基于以上分析,设计如下实验:随机生成50个城市的坐标,蚂蚁的数量为50只,ρ=0.5,β=5,迭代次数IMax=200,α的取值范围为[0.4,0.5,0.8,1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0]。测试结果如图3所示,当α的取值小于1时,信息素浓度的作用被抑制,迭代时间较长(绿色虚线);当α的取值大于1时,收敛时的最短距离偏大(蓝色实线),且最短距离随着α的增大有变大趋势,说明这种情况下得到的更多是局部最优解。根据多次测试与观察,α的最佳取值范围在[1.0,4.0]之间,这个时候可以达到搜索质量与速度的平衡。
2.4.3启发式因子β
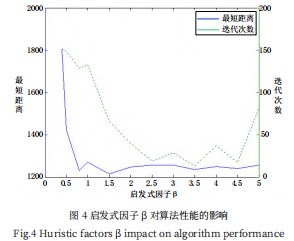
启发式因子β在公式(1)中对节点间的能见度ηij有强化作用,倾向于短路径节点的选择,反映了一种自然选择策略,即优先选择距离近的节点,体现了先验性和确定性的重要程度。如果β值较小,整体算法的随机性会变强,虽然更能生成全局最优解,但迭代时间变长;如果β值较大,搜索算法的确定性变强,偏向选择局部最短路径,不易找到最优路径。基于以上分析,设计如下实验:随机生成50个城市的坐标,蚂蚁的数量为50只,ρ=0.5,α=1,迭代次数IMax=200,β的取值范围为[0.4,0.5,0.8,1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0]。测试结果如图4所示,随着β值的增大,算法确定性逐步增强,最短距离和迭代时间都有减少的趋势。最短距离在β值处于[2.5,5]时进入平缓状态。根据多次测试与观察,β的最佳取值范围在[2.5,5]之间,这个时候可以达到搜索质量与速度的最佳。
2.4.4参数组合
蚁群算法一方面要求获得全局最短距离,另一方面要求算法收敛速度更加高效。由前面的算法参数分析可知,每一个参数的值都有相应的取值范围,对算法性能都有较大的影响,且参数与参数之间有相互提升和抑制的作用。为了得到算法性能和效率的整体提升,对α、β作组合测试。基于以上分析,设计如下实验:随机生成50个城市的坐标,蚂蚁的数量为50只,ρ=0.5,迭代次数IMax=200,α取值范围在[1.0,2.0,3.0,4.0]之间,β取值范围在[3.0,4.0,5.0]之间,计算得出共有4×3=12种组合。测试结果如图5所示,横轴1_3表示α=1,β=3,横轴1_4表示α=1,β=4,以此类推。在图5中,随着α、β的逐渐增大,计算所得的最短距离(蓝色实线)整体呈递增趋势,所需的迭代时间(绿色虚线)整体呈递减趋势。可以解释为随着α、β值的增大,算法确定性越来越强,多样性越来越差,造成迭代时间缩短,获取的是局部最优解。根据多次测试与观察,α=1,β=5,这个时候可以达到搜索质量与速度的最佳。在图5中,α=1,β=5对应的纵轴值基本处于最低位。
3蚁群算法的改进
3.1蚁群算法存在问题
根据蚁群算法的原理和模型,以及其在实际生产中的应用表现,其存在以下问题和缺陷[13]:
(1)收敛速度较慢。初始状态所有节点之间的信息素量相等,且从一个节点选择下一个节点的方法具有较大的随机性,虽然有利于搜索全局最优解,但时间积累成本较大,延缓了整体的收敛速度。在TSP算法实现中,往往需要多轮迭代才能得到环游最小距离值。
(2)陷入局部最优问题。蚁群算法虽然引入了信息素的积累作为指引蚂蚁前进的参考和依据,使路径选择不断朝正反馈加强的方向进行,但易陷入局部最优解的情况。特别是当信息素挥发因子ρ等相关参数设置不当,导致某些位置信息素量积聚,越来越多的蚂蚁朝这个方向,使搜索陷入次优解或是停滞。
(3)搜索过程易形成闭环路。正是蚁群算法在择路中具有不确定性,使整个搜索过程在一定概率情况下形成子环路。通过设定访问节点禁忌表可以缓解这个问题,但在某些场景下,使用禁忌表也会发生死锁现象。
(4)参数优化缺乏一致性标准。蚁群算法涉及一组参数,包括蚂蚁的个数、启发式因子α和β、信息素挥发系数ρ、初始信息素量等。这些参数具有关联相关性,在不同的城市个数及距离背景下,需要通过不断调整获得待求问题的最佳参数组合。
(5)最优解和收敛速度之间的平衡。最优解具有全局性,避免过早的信息素分布不均匀,防止因城市数量规模扩大时算法易进入局部最优解而产生“早熟”[14]的计算结果,这些都要求更多的迭代和计算。蚁群算法需要在最优解和收敛速度之间达成平衡。
3.2蚁群算法的改进
基于蚁群算法存在的问题,可以从信息素初始化、信息素更新规则、参数优化设置、路径选择算法、路径搜索策略等途径进行改进。文献[15]提出一种改进信息素二次更新局部优化蚁群算法(IPDULACO),实验证明,通过二次更新信息素、跳出局部最优解等措施,该方法能够在较少的迭代次数内获得更精确的解,从而具备更强的全局搜索能力和更快的收敛速度。
4结语
路径规划广泛应用于日常生活生产中。本文以TSP问题为研究对象,讨论了蚁群算法的原理,并分别使用蚁周模型、蚁量模型、蚁密模型的定义给出了蚁群算法的实现。通过对蚁群算法的参数分析,找出特定场景下的最优参数组合。最后研究讨论了蚁群算法存在的问题及改进途径。实验结果表明:相对于蚁量模型和蚁密模型,蚁周模型具有更强的全局搜索能力;组合参数优化有利于蚁群算法的收敛;可以从信息素初始化、信息素更新规则、参数优化设置、路径搜索策略等途径改进蚁群算法。
参考文献
[1]刘砚菊,杨青川,辜吟吟.蚁群算法在机器人路径规划中的应用研究[J].计算机科学,2008,35(5):263-265.
[2]仪孝展.基于改进遗传算法的物流车辆路径规划方法研究与应用[D].西安:西安理工大学,2018.
[3]伟伟,王伟,陈能成,等.一种利用改进A*算法的无人机航迹规划[J].武汉大学学报(信息科学版),2015,40(3):315-320.
[4]尚兴宏.无线传感器网络若干关键技术的研究[D].南京:南京理工大学,2013.
[5]黄辰,费继友,刘洋,等.基于动态反馈A*蚁群算法的平滑路径规划方法[J].农业机械学报,2017,48(4):34-40.
[6]宋彬.结合粒子群算法和改进蚁群算法的机器人混合路径规划[D].徐州:中国矿业大学,2018.
[7]荀燕琴,田竹梅,任国凤,等.基于遗传算法的智能扫地机器人路径规划研究[J].高师理科学刊,2020,40(3):56-60.
[8]许亚.基于强化学习的移动机器人路径规划研究[D].济南:山东大学,2013.
[9]王沛栋.改进蚁群算法及在路径规划问题的应用研究[D].青岛:中国海洋大学,2012.
[10]崔志华,孙佑强,任叶青.改进蚁群算法在机器人路径规划中的应用[J].南昌工程学院学报,2020,39(1):15-19+24.
[11]刘军.基于改进蚁群算法的移动机器人路径规划研究[D].郑州:郑州大学,2010.
[12]王胜训.蚁群算法的改进及TSP仿真研究[D].西安:西安电子科技大学,2014.
[13]张松灿,普杰信,司彦娜,等.蚁群算法在移动机器人路径规划中的应用综述[J].计算机工程与应用,2020,56(8):10-19.
[14]吴华锋,陈信强,毛奇凰,等.基于自然选择策略的蚁群算法求解TSP问题[J].通信学报,2013,34(4):165-170.
[15]许凯波,鲁海燕,程毕芸,等.求解TSP的改进信息素二次更新与局部优化蚁群算法[J].计算机应用,2017,37(6):1686-1691.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/49465.html