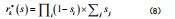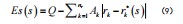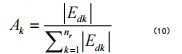SCI论文(www.lunwensci.com):
摘要:含分布式电源的配电网会产生短路、电压骤降等各种问题,为提升电能质量水平,工作人员需进行更加精确的扰动源位置确定。而通过矩阵方式,对配电网拓扑结构、电能质量监测中的相关信息进行描述,能基于遗传算法的模型构建,以及MATLAB仿真,将分布式电源接入,在该算法的帮助下自动精确定位接入分布式电源。
关键词:分布式电源;配电网;电能质量
Research on location of power quality disturbance source in distribution network with distributed generation
Wang Weisheng
(Hangzhou Decheng Electric Power Technology Co.,Ltd.,Hangzhou Zhejiang,310000)
Abstract:The distribution network with distributed power generation will cause various problems such as short circuit and voltage sag.In order to improve the level of power quality,the staffneeds to determine the location of the disturbance source more accurately.Through the matrix method,the distribution network topology structure and relevant information in power quality monitoring can be described,which can be based on genetic algorithm model construction and MATLAB simulation to connect distributed power sources and automatically and accurately locate with the help of the algorithm.Access to distributed power.
Key words:distributed power supply;distribution network;power quality
近年来,我国分布式电源的发展十分迅速,电力短缺、能源结构等问题因此得到缓解,但是在传统电力系统优化与控制方面却面临极大的挑战。目前,在国内外研究中,分布式电源(DG)技术已成为研究热点,同时,电能质量的扰动源定位备受关注。若电能质量问题能快速解决,则能降低经济损失。
一、扰动源定位原理与电能质量监测仪误判
(一)矩阵算法原理
扰动源的定位应以配电网信息为基础,发挥矩阵算法的作用,而定位的内容包括配电网拓扑关系和电能质量监测仪(PQM)等。同时,扰动源定位能判定扰动事件发生时的扰动方向[1]。结构和监测点布置信息可以使用结构举证Cl×m进行表示:

式中,l、m、PQM、Cij分别为系统中的线段数量、系统中实配PQM与虚拟PQM的总数第i条线段与第j个PQM的位置关系。
扰动方向判别矩阵可以使用PQM的方向判定信息予以确定,计为Dm×1。
j的取值为1到m的正整数
矩阵运算可以综合结构信息与方向判定信息,然后得到结果矩阵Ri×1=Cl×mDm×1,元素可以表示为:
元素ri在扰动源位置为Li时,可以确定其对应关系为Cijdj,为1×1或(-1)×(-1),这时可以确定ri=m。在元素ri的累加式中,Li不是扰动源位置,这样Cijdj为1(-1)或(-1)×1,确定ri<m。当ri=m时,Li为扰动源所在位置。
(二)PQM方向误判
在电压暂降过程中,方向盘点主要运用的是扰动能量法,还需用到扰动功率的计算;在对谐波源进行判定时,使用的方法为谐波功率,可以利用闪变功率对电压闪变方向进行判定[2]。
主要有两个方面的原因造成PQM方向误判,具体如下:第一,潮流方向受到DG影响后会产生改变,借助扰动能量法进行分析,获取的结果表现为正负极性,会有倒转结果发生;第二,在状态估计时,虚拟PQM出现计算误差,这也会造成误判。
扰动功率、扰动能量要求能在暂态扰动期间确定,二者分别为PD、ED,线路潮流输送方向在DG有功位置的力较大时,按照下面的公式进行计算:
式中
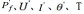
分别为DG接入后的扰动期间三相有功功率、DG接入后的稳定电压、DG接入后的电流、DG接入后的功角、扰动持续时间。
二、扰动源定位新方法
以遗传算法为基础定位扰动源,利用PQM检测仪,可获取电流(以i表示)与电压(以u表示)的相关信号,并对扰动源相对于检测仪的位置进行检测。通过遗传算法,可按照检测仪与扰动源相对于监测仪的位置进行定位[3]。
当群体内有适应值Q的个体时,可作为遗传算法中收敛的重要条件。各监测点需要在单个扰动共同形成后,对其状态进行监测,要求适应度函数最大,最优解可以输出,约束条件需进行明确[4]。当线路状态之和为1与线路状态之和为0时,可以表示不同的内容,对应的分别为扰动源所在线路、电源、出口母线等[5]。
在对扰动源进行定位时,要按照下面的步骤操作。
首先,监测设备中有大量数据,将这些监测到的数据提取出来,通过编号,确定出在扰动方向为前向、后向扰动时,编号明确为1、0,然后建立适应度函数,即:
式中Q、nr、s、n、rk、Ak分别为一个较大的整数、监测点数量、线路状态向量、维数、第k个监测点状态、第k个监测点扰动方向信息监测函数、第k个监测点扰动权值参数[6]。
其次,在监测点上游线路中,并无扰动源的存在,而在下游线路可发现扰动源,这样可以确定监测点函数对应值为1,反之为0,然后对第k个监测点的监测函数进行计算:
式中:si、sj分别为监测点k上游方向第i条线路的状态、监测点k下游方向第j条线路的状态。
再次,扰动方向结果显示,当监测点处的扰动信号较低时,结果往往不够精准,因此,监测点扰动信号要在信号比较强时赋予其偏大的权值即第k个监测点状态的比例权值[7]。
式中Edk为第k个监测点在扰动完成后的高频扰动能量。
最后,最佳适应度函数值可以在遗传算法下计算得出,解码种群最佳解能对动源初始位置进行确定,检测出线路是否有监测盲区存在,如果存在盲区,需对定位结果进行扩展。
三、仿真分析
(一)仿真模型
100MVA的IEEE14节点配电网是基准容量中的重要节点,对其进行仿真,并开环进行系统运行。将3处DG接入后,利用MATLAB仿真软件构建配电网模型,并对其进行算法编程。为降低成本,PQM的配置十分有限[8]。例如,实际配置的PQM数量为10个,通过状态估计得到虚拟PQM数量为3个。在配置时需遵循的基本原则为:将实际PQM配置于与DG母线直接相连的线段,对于其他普通母线,一般情况下虚拟PQM的配置只有一个。对于评价函数的虚拟PQM补偿系数,取值需控制在0-0.5之间[9]。
(二)监测点的覆盖范围
监测点的覆盖范围见表1。
监测期间出现三个盲区,盲区1为L1、L5;盲区2为L2、L10;盲区3为L3、L12。可以得到各监测点的状态为:r=(1,0,0,1,0,0,0,0,0,0)。各监测点的扰动权重为:A=(0.0751,0.0007,0.00 047,0.1210,0.7885,0.0030,0.000,0.0011,0.0014,0.0034)。在遗传算法后,初始染色体为20个,迭代100次,可以得到在Pc、Pm处分别为0.65、0.05,由此可以精确确定扰动源位置,发现位置为L4[10]。
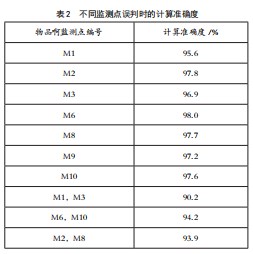
为对遗传算法的准确性进行有效验证,本文通过多组实验,对在L4发生三相短路情况时是否发生扰动方向误判进行分析,通过计算可以得到下面的结果(见表2)。
从表2可以看出,通过遗传算法对扰动源位置进行判断发现其准确度较高,当1个监测点误判时,准确度保持在95%以上,当2个监测点扰动方向误判时,准确度在90%以上。在对扰动源进行定位时,遗传算法的应用效果较好。只有1个监测点误判时,准确度提升范围为0.10%~2.84%,有2个监测点误判时,准确度提升范围为2.84%~4.69%。
四、结语
在分析高频扰动能量正负、相关扰动方向的过程中,可以通过遗传算法构建适度函数,对扰动源进行精准定位。通过MATLAB的应用进行仿真分析,可发现遗传算法下的函数计算具有较高的定位精准度。虽然电能质量扰动源定位得到快速发展,但研究依然不够成熟,还有许多需要完善的地方,希望未来对扰动源进行定位时能有一种高效定位扰动源的简便方法。
【参考文献】
[1]谢林枫,王红星,刘军成,尹飞,仲春林,梁栋.基于电能质量约束的智能配电网分布式电源消纳能力研究[J].电网与清洁能源,2020(4).
[2]王惠文,牛轲,王思敏.分布式电源不确定性的配电网系统可靠性评估方案探讨[J].微型电脑应用,2019(5).
[3]谭笑,王主丁,李强,庞祥璐.计及多约束的多分布式电源接入配电网最大承载力分段算法[J].电力系统自动化,2020(4).
[4]颜湘武,徐韵,李若瑾,金永盛,李铁.基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化[J].电工技术学报,2019(10).
[5]徐艳春,樊士荣,谭超,李振华,吕密.基于改进EWT-CMPE的高渗透率主动配电网电能质量扰动检测与分类[J].电网技术,2020(10).
[6]石玉东,蒋卓臻,高红均,王家怡,朱嘉远.促进风电消纳的配电网分布式电源与电动汽车充电站联合鲁棒规划[J].可再生能源,2018(11).
[7]苗友忠,李顺昕,雷为民,何洛滨,吕昕.考虑用户负荷类型的含分布式电源的配电网可靠性评估[J].电力科学与技术学报,2020(2).
[8]李腾,葛少云,梁文举,周鑫,孙洪波.考虑环境效益的含分布式电源配电网概率可靠性评估[J].电力系统及其自动化学报,2019(1).
[9]王巍璋,王淳,尹发根.基于可达矩阵和贝叶斯定理的含分布式电源的配电网故障区段定位[J].中国电力,2021(7).
[10]董新,李莉,李嫣然,于光波,巩晓静.基于有序二元决策图的分布式电源组网重构及其r对配电网风险水平的影响[J].电力系统保护与控制,2018(016).
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/42839.html



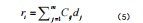
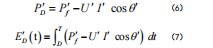
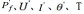 分别为DG接入后的扰动期间三相有功功率、DG接入后的稳定电压、DG接入后的电流、DG接入后的功角、扰动持续时间。
分别为DG接入后的扰动期间三相有功功率、DG接入后的稳定电压、DG接入后的电流、DG接入后的功角、扰动持续时间。