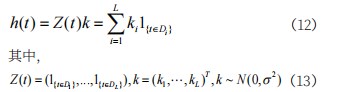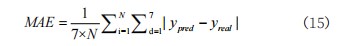SCI论文(www.lunwensci.com):
摘要:时间序列数据的预测,因时间特征的动态多种变化性,一直是预测问题中的难点。传统的时间序列预测方法,如Arima方法,数据需要满足的条件较多,建模前期对数据要做较为复杂的预处理,在应用上有很大的限制。本文使用Facebook开源的时间序列预测框架fbprophet,以郑州地铁客流量数据为研究对象,对其建行了流量预测,这一预测能为加强地铁管理提供数据支持。通过与Arima方法比较,fbprophe在表现上更优。实验结果表明,fbprophe在情况复杂,多种节假交叉影响的数据集上都更好的得到准备确的预测结果。
关键词:时间序列;Arima;fbprophe
Research on Time Series Analysis Based on Prophet Software
PAN Weiquan,LI Jiajia,FAN Dongmei
(School of Mathematics and Statistics,Yulin Normal University,Yulin Guangxi 537000)
【Abstract】:The prediction of time series data is always a difficult problem because of the dynamic variability of time characteristics.Traditional time series prediction methods,such as Arima method,have a lot of requirements for data to meet.In the early stage of modeling,the data needs to be preprocessed in a complex manner,which has a great limitation in application.In this paper,fbprophet,an open source time series prediction framework of Facebook,is used to take the passengerflow data of Zhengzhou subway as the research object to predict its traffic construction,which can provide data support for strengthening subway management.Compared with the Arima method,fbprophe is superior in performance.The experimental results show that fbprophe can get better prepared prediction results on the data sets with complex conditions and multiple seasonal and pseudo-crossing effects.
【Key words】:the time series;Arima;fbprophe
1研究方法
1.1 Prophet模型预测原理
Prophet算法是可分解的时间序列算法,主要由三部分构成,分别是趋势项、季节性趋势、节假日。它使我们能够使用简单直观的参数准确地进行时间序列的预测,并支持包括自定义季节和假日的影响。由此可见,Prophet相比现有预测工具更加人性化,生成的预测结果足以和专业分析媲美。因此,本文利用Prophet算法对地铁流量进行预测。
Prophet的一般形式可以表示为:
y(t)=g t()+s(t)+h(t)+εt(1)
其中,g(t)表示趋势项,用来拟合非周期性变化的趋势。s(t)用来表示周期项,比如说每周、每年、季节等。h(t)表示假期项,表示当天是否存在节假日,最后εt表示误差项,用它来表示随机无法预测的波动。
在Prophet算法里面,趋势项g(t)有两个重要的函数,一个是基于逻辑回归函数,另一个是基于分段线性函数。首先,我们来介绍逻辑回归函数:

其中,C表示曲线的最大渐进值,k表示曲线的增长率,m表示曲线的中点。当C=1,k=1,m=1时,恰好就是Sigmoid函数的形式,满足微分方程:y'=y(1-y)。当适用分离变量法来求解微分方程y'=y(1-y)时,可以得到:

但是,在现实生活中,函数f(x)=C/(1+e−k(x−m))的三个参数C,k,m很有可能是随着时间变化的。因此,需要把这三个参数全部换成随时间变化而变化的函数,即C=C(t),k=k(t),m=m(t)。
在现实的时间序列中,曲线的走势不会一直保持不变。当在某些特定的时候或者有着某种潜在的周期时,曲线会随之发生变化,引起曲线变化的点称为突变点。于是我们可以设有S个变点,且变点的位置是在时间戳sj,1≤j≤S上,那么在这些时间戳上,我们需要给出增长率的变化。此时,假设有这样一个向量:δ∈Rs,其中δj表示在时间戳sj上增长率的变化量。由于k表示增长率,所以在时间戳t上的增长率就是

通过一个指示函数a(t)∈{0,1}S就是:

k是增长率,δ是适应量,m是偏移量参数。
季节性趋势使用傅里叶级数来模拟时间序列的周期性。假设P表示时间序列的周期,P=365.25表示以年为周期,P=7表示以周为周期。傅里叶级数的形式是:

因此,时间序列的季节项就是:s(t)=X(t)β,而β的初始化是β~N(0,σ2)。
由于每个节假日对时间序列的影响程度不一样,例如春节、国庆节是七天的假期,五一、中秋等则是比较短的假期。因此,不同的节假日可以看成相互独立的模型,并且可以为不同的节假日设置不同的前后窗口值,表示该节假日会影响前后一段时间的时间序列。假设有L个节假日,则
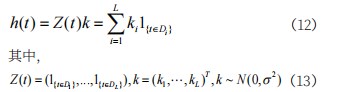
其中,Di表示节假日的前后一段时间,ki表示节假日的影响范围。
1.2 ARIMA模型预测原理
ARIMA(Autoregressive Integrated Moving Average)模型简称差分自回归移动平均模型,是由Box与Jenkins于20世纪70年代提出来的,包括自回归模型(简称AR模型)、移动平均模型(简称MA模型)和自回归移动平均模型(简称ARMA模型),是一种著名的时间序列预测算法。
ARIMA(p,d,q)模型是由MA(q)模型、AR(p)模型和差分法结合得到的,其中d是时间序列成为平稳时所做的差分次数。一般形式如下:

建立ARIMA模型的一般分为以下4个部分:(1)时间序列平稳性检验;(2)模型的识别也称为模型的定阶;(3)参数估计和模型检验与评价;(4)模型拟合及应用。
采用以上方法构建的最优预测模型拟合郑州市2015年8月—11月共115天郑州市地铁的客流量。本文通过计算均方误差(其值越小,该模型预测效果越好)来评价建立的模型预测效果。
2应用实例
本文是以郑州地铁客流量为研究对象,采用的数据包括郑州市2015年8月—11月共115天郑州市地铁线路刷卡记录(https://github.com/ljj1218652992/-)。由于原始数据量过大,无法正常对数据进行操作,观察数据变量,根据预测所需的变量删除部分无关变量,因此利用统计软件R,将全部数据按日分成115个Excel文件,每天的数据作为一个Excel文件,便于快捷的对后期数据进行处理。再提取TRADE_TYPE(刷卡类型编号:21、22)进行每个站点(20个站)每日的日客流量,得到一个20列115行的矩阵,包含了20个站点每日的客流量。
将统计出来的各站点数据进行初步建模,在Prophet中进行要简单易懂得多,输入已知的时间序列的时间戳和相应的值;输入需要预测的时间序列的长度;便可输出未来的时间序列走势,其输出结果可以提供必要的统计指标,包括拟合曲线、上界和下界等。按照此步骤对Prophet进行初步的建模得到未来的时间序列走势展示图如图1所示。
通过观察图1发现有些点不能得到很好的拟合,随后利用R语言stats包检测出异常的离群点,分析和查找资料后发现这些异常点对应的时间点都是2015年郑州市的节假日前后的时间点。
假期和突发事件会对时间序列产生可预测的冲击,在节假日前后地铁客流量总会比往日增多,导致数据异常对模型产生影响,预测出来的数据误差会增大。
那么,要如何处理这种情况,在时间序列的其他模型中要处理这种节假日的情况要艰难得多,而Prophet处理节假日等突发事件的情况相对于要简单易操作。比如,查找资料分析异常数据发现突然暴增的地铁客流量都与2015年8月—11月的假期有关,因此我们对节假日进行设置,设置了开学、中秋节、国庆节、反法西斯抗战胜利60周年等几个节假日,并对季节性效应、周效应等周期性变化进行调控,得到最优模型结果预测图,如图2所示。
构建ARIMA(p,d,q)模型要先进行数据平稳性检验,因此将整理出各站点的日客流量数据,进行ADF检验,发现只有143站点的数据不平稳,因此对该站数据取对数后达到了平稳。R语言Forecast包中的auto.arima
函数可以快速确定ARIMA(p,d,q)模型最优的p,d,q。因此利用该函数得到143站点的最优模型为ARIMA(2,1,2),根据已知的p,d,q构建模型进行预测,预测7d数据。其余站同样进行预测,最终得到一个7行20列的预测矩阵。为更加直观的观察模型结果,以143站点为例展示其最优ARIMA模型结果如图3所示。
从图1中可以明显观察到模型拟合的情况,发现有些浮动的异常点,因为时间序列通常会随着天、周、月、年等季节性的变化而呈现季节性的变化,也称为周期性的变化,通常要经过具体分析才能确定。Prophet虽然不能观察得到它是否具有季节性趋势、节假日效应以及周效应等周期性变化,但是它较为独特的优点之一是,可以默认通过傅里叶级数来自动调整季节效应、节假日效应以及周效应,从而快速而准确的得出预测结果,这一优点是其他预测时间序列的模型所不具备的。
从图2观察可以看出,设置了节假日、调整了季节性效应、周效应等周期性变化参数后的模型拟合结果明显要比图1没有调整的时候好了许多。
当发现预测的模型跟与计划中的存在偏差,预测模型未按计划运行时,我们希望能够针对眼前的具体问题调整方法的参数。若是在时间序列其他模型中,想要调节上述中因节假日问题以及要依靠具体分析后才能确定的季节性效应、周效应等周期性变化,不是专业人士分析,大部分人都是不大懂得如何处理。
在Prophet中就不一样了,在不了解的情况下默认傅里叶级数自动调整,经过具体分析后,它可以通过调节季节性影响的参数大小,在Prophet中,时间序列的季节项就是:S(t)=X(t)·β,而β的初始化是β~N(0,σ2)这里的σ是通过seasonality_prior_scale来控制的,也就是说σ=seasonality_prior_scale。这个值越大,表示季节
的效应越明显 ;这个值越小,表示季节的效应越不明显。
在现实环境中,除了周末,同样有很多节假日,而且不同的国家有着不同的假期。在Prophet里面收集了各个国家的特殊节假日。除了节假日之外,用户还可以根据自身的情况来设置必要的假期,例如2015年反法西斯60周年、开学等。设置了现实环境中具体节假日的时间段,使得模型拟合得更好,预测结果更加精准,具体哪个更加准确将在接下来的模型结果分析中具体分析。
从图3 ARIMA预测结果图可以粗略观察到其预测趋势符合整体数据的走势,且整个流程走下来,同样不能观察得到它是否具有季节性趋势、节假日效应以及周效应等周期性的变化,但是其却不具备Prophet傅里叶级数自动调节的优点,要经过具体分析才能确定。
3结果对比
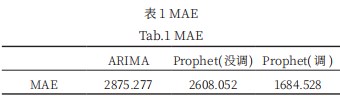
为了使结果更具有说服力,计算各算法预测结果的误差,采用的是MAE均方误差进行计算,其计算公式如下:
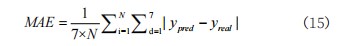
通过R对预测结果进行误差计算,Prophet预测结果分为没调整季节项参数也没设置节假日的情况下的预测结果,以及调整后的预测结果进行MAE计算,得到如表1所示:
通过表1可以看出ARIMA的预测结果MAE达到2875.277是调整到最优的p,d,q模型后得出的预测结果,再看Prophet没有调整任何参数也没有设置节假日或者突发事件的情况下的MAE为2608.052比ARIMA的MAE小了267.225的误差值,Prophet调整参数和设置节假日、突发事件后的预测结果误差缩小923.524,显而易见的Prophet的预测结果要比ARIMA精准,由此可以得出结论Prophet能够生成快速而准确的时间序列预测。
4结语
本文详细介绍了ARIMA模型和Prophet模型。以郑州地铁客流量为研究对象,选取2015年8月—11月共115天的客流量数据,将数据分为训练集与测试集,然后分别训练ARIMA、Prophet模型,最后计算均方误差进行模型对比,预测结果的均方误差分为2875.277和2608.052。由此可知,相比于传统的时间序列模型ARIMA,Prophet模型的预测效果更佳。由于Prophet预测模型的参数非常容易解释和调整,即使缺乏专业知识的人来做预测也可准确的做出调整,使模型对现实中的各种问题做出有意义的预测。因此,本文对Prophet模型调整了参数,把一些节假日、突发事件设置为突变点,再进行模型预测,均方误差降为1684.528。Prophet算法不仅可以处理时间序列存在一些异常值的情况,也可以处理部分缺失值的情形,还能够几乎全自动地预测时间序列未来的走势。因此,如果是一般的商业分析或者数据分析的需求,都可以尝试使用这个开源算法来预测未来时间序列的走势。
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/41686.html



 通过一个指示函数a(t)∈{0,1}S就是:
通过一个指示函数a(t)∈{0,1}S就是: