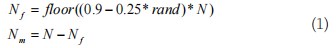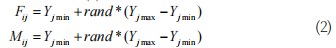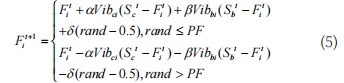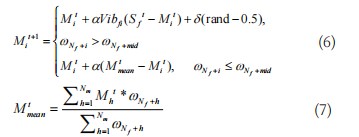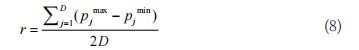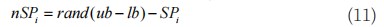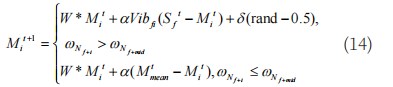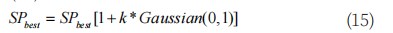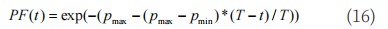SCI论文(www.lunwensci.com):
摘要:为改善群居蜘蛛优化算法中存在的收敛速度较慢和收敛精度低的问题,提出基于混沌映射与高斯变异的群居蜘蛛优化算法。首先,在种群初始化过程中采用混沌映射反向学习策略;其次,蜘蛛位置更新过程中引入自适应权重和动态概率因子;最后,在种群完成交配操作后,针对蜘蛛群中最优个体位置进行高斯变异扰动。通过实验证明:改进后的算法在测试函数上能够做到快速收敛,同时函数的最终收敛精度得到明显提高。通过30维与50维的实验结果可以看出,改进后的算法对于不同维度的函数都有着较好的收敛精度。
关键词:群居蜘蛛优化算法;高斯变异;混沌映射;动态概率因子;收敛精度
Social Spider Optimization Algorithm Based on Chaos Mapping and Gaussian Mutation
YE Kuntao,GAO Haiyi,LI Sheng
(College of Science,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000)
【Abstract】:To improve the problems of slow convergence rate and low convergence accuracy existing in the gregarious spider optimization algorithm,a social spider optimization algorithm based on chaos mapping and gaussian mutation is proposed.Firstly,the chaotic mapping reverse learning strategy is adopted during population initialization;Secondly,adaptive weights and dynamic probability factors are introduced in the spider position update;Finally,gaussian variation is disturbed for the optimal individual position in the spider group.Experiments show that the improved algorithm can converge quickly in the test function,and thefinal convergence accuracy of the function is significantly improved.The experimental results of 30 dimensions and 50 dimensions show that the improved algorithm has a good convergence accuracy for the functions of different dimensions.
【Key words】:social spider optimization;gaussian mutation;chaos mapping;dynamic probability factor;convergence accuracy
0引言
群居蜘蛛优化算法(Social Spider Optimization,SSO)是国外学者Cuevas E[1,2]等人通过自然界中蜘蛛种群中个体之间的协作提出的一种新型群智能优化算法。相较于经典的粒子群优化算法[3]、蜂群算法[4]等具有较好的收敛速度和全局搜索能力。但同其他群智能算法一样,SSO算法随着迭代次数的增加,雌雄蜘蛛的种群多样性降低,算法容易陷入局部最优,全局搜索能力降低,最终使得算法收敛速度慢、收敛精度低。因此,近年来,部分学者针对SSO算法存在的不足进行了相应的研究。2017年,王丽[5]等人在求解多峰函数过程中引入了自适应决策半径概念,证明了提出的AMBSSO算法在多峰函数问题求解的优越性。2020年,Yang W[6]等人通过引入子种群的动态更新机制、高斯交配半径和多定时策略提出ISSO算法,平衡了算法的全局搜索与局部搜索能力。2021年,向蕾[7]等人将SSO算法与粒子群算法相结合来优化算法收敛度。这些改进的算法,一定程度上改善了全局搜索能力和局部搜索能力的平衡,同时收敛速度、收敛精度也有一定提高,但是这些改进的算法能力依然不足,仍然存在全局搜索能力与局部搜索能力的平衡不足,收敛速度较慢和收敛精度低的问题。为了解决上述问题,使得算法全局搜索能力提高,收敛速度快、收敛精度提高,本文提出了一种混沌映射与高斯变异的群居蜘蛛优化算法(Social Spider Optimization Algorithm Based on Chaos Mapping and Gaussian Mutation,GSSO)。
1标准SSO算法
在标准SSO算法中,将自然生物学中的蜘蛛网模拟为优化问题中解的空间范围,此时,在蜘蛛网上的所处的位置就等同于优化问题的一个解,通过雌雄蜘蛛个体间相互协作完成优化问题的求解[8-12]。标准SSO算法主要通过以下步骤实现优化问题的解决:
(1)蜘蛛种群初始化。随机在D维优化求解空间中分布由N个蜘蛛构成的蜘蛛种群SP,其中,雌性与雄性蜘蛛数量Nf、Nm计算公式如(1)所示。
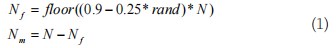
式中,rand为[0,1]随机数。其中,不同性别的蜘蛛个体通过公式(2)生成:
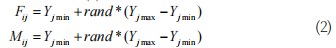
式中,Fij为雌性蜘蛛个体Fi第j维变量,Mij为雄性蜘蛛个体Mi第j维变量,Yjmax、Yjmin表示蜘蛛中当前维变量的上限和下限。
(2)计算蜘蛛权重值。在标准SSO算法中,通过引入权重值来模拟蜘蛛的大小,权重值ω通过蜘蛛个体适应度值计算如式(3)所示:

(3)计算蜘蛛振动力。在蜘蛛网中,蜘蛛个体通过在蛛网上振动来与其他个体产生信息交流。为了模拟该过程,由蜘蛛个体j根据公式(4)建立与个体i间传递信息而感知到的振动力:

式中,di,j通过欧拉公式进行计算。
(4)雌性蜘蛛更新方式。雌性蜘蛛主要通过振动来决定对其他个体产生吸引或排斥操作,以此来完成蜘蛛位置更新过程。定义个体Fi更新方式如式(5)所示:
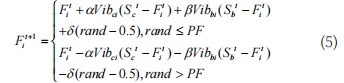
式中,α,β和rand是[0,1]区间内的随机数;Sc代表相距蜘蛛Fi最近同时满足其权重高于Fi的蜘蛛;Sb代表整个种群中最好的蜘蛛所在的位置;Vibci代表蜘蛛个体Fi对个体Sc的震动感知力;Vibbi代表蜘蛛个体Fi对个体Sb的震动感知力;PF为概率因子。
(5)雄性蜘蛛更新方式。雄性蜘蛛主要分为两种:位置优越的主动型蜘蛛和位置较差的被动型蜘蛛。依据平均惯性权重来决定雄性蜘蛛个体Mi更新方式,如式(6)所示(以最小值优化问题为例):
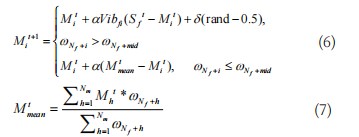
式中,ωNf+mid为雄性蜘蛛种群中权重值的中位数;Sf为与蜘蛛Mi相距最小的雌性蜘蛛个体;Vibh代表蜘蛛个体Mi对个体Sf的震动感知力。Mtmean为所有雄性蜘蛛的中间位置如式(7)所示。
(6)雌性蜘蛛与雄性蜘蛛进行交配操作。对于位置优越的主动型雄性蜘蛛,在交配半径r内查找是否存在雌性蜘蛛。交配范围内存在雌性蜘蛛时,雌性蜘蛛与该雄性蜘蛛构成集合TG;否则,交配操作将取消。交配半径r根据公式(8)计算:
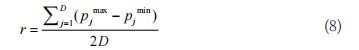
式中,pmaxj和p为第j维变量的上限和下限。在交配过程中,蜘蛛权重值决定了其进行交配的概率。在集合TG内,蜘蛛个体的交配概率Pi根据轮盘赌计算,由每只蜘蛛个体的权重值决定,具体由公式(9)定义:

即权重值大的蜘蛛发生交配的概率高,而权重值小的个体交配的概率低。
如果交配产生新蜘蛛SPnew的权重值优于种群中最差蜘蛛SPworst权重值,则新蜘蛛SPnew将会替代最差的蜘蛛SPworst,否则,新蜘蛛SPnew就会被丢弃,种群不发生变化。在替换过程,要求新蜘蛛SPnew的性别与被替换蜘蛛相同,这样可以保证整个种群SP中雌性与雄性蜘蛛之间的原始数量比保持不变。
2群居蜘蛛优化算法的改进
2.1混沌映射反向学习初始化种群
在标准SSO算法中,对于蜘蛛位置的初始化采用的是在上下限范围内机取值。这种方法操作上简单,但存在着一定的缺点,不能保证初始位置均匀分布,使算法的最优值以及收敛速度都得不到很好的效果。因此,本文利用Logistic映射与反向学习相结合的方法进行种群初始化[13],使蜘蛛个体的初始位置能更加均匀地分布,具体实施步骤如下:
(1)利用混沌映射如式(10)所示生成N个蜘蛛初始位置SPi;

式中,μ为混沌参数,其取值范围为μ∈(2,4],μ在越接近4的过程中,种群更易平均分布。
(2)将上式生成的N个初始解SPi按式(11)所示生成相对应的N个反向初始解nSPi;
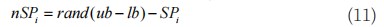
式中,ub和lb为当前蜘蛛所在位置的上下界。
(3)在求解最小值的优化问题中,将生成2N个SPi和nSPi的蜘蛛所在位置的函数适应度值进行顺序排列,选择前N个值作为初始化的蜘蛛群。
2.2自适应权重的位置更新
在标准SSO算法中,雌性与雄性蜘蛛的位置更新过程可以看出,蜘蛛更新后的位置受当前位置的影响很大。在雌雄蜘蛛位置更新过程中,引入自适应权重来动态平衡全局搜索和局部搜索,能够提高算法的搜索速度和收敛精度[14,15],自适应权重W如式(12)所示:

式中,T为算法设置的终止迭代次数,t为当前迭代次数。改进后,雌性蜘蛛位置迭代方式如式(13)所示:

雄性蜘蛛位置迭代方式如式(14)所示:
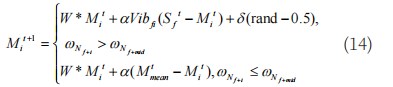
式中变量含义同公式(5)、式(7)相同。
2.3高斯变异
在标准SSO算法中,算法在迭代过程中,会随着迭代次数的增加,种群中蜘蛛位置的多样性降低,从而使其陷入局部最优,因此,在种群完成交配操作后,针对蜘蛛群中最优个体位置SPbest进行高斯变异扰动[16-17],如式(15)所示:
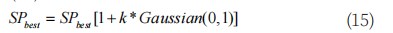
式中:SPbest是蜘蛛最优个体的位置;k为l到0之间随机数;Gaussian(0,1)表示服从均值为0方差为1的高斯分布的随机向量。
2.4动态概率因子
在标准SSO算法中,概率因子PF是雌性蜘蛛位置更新中重要的影响参数,固定的概率因子不能起到平衡雌性蜘蛛在位置更新时的吸引与排斥操作。通过动态概率因子来替代固定概率因子,当PF较小时,雌性蜘蛛中进行吸引操作的概率变小,提高全局搜索能力,当较大时,雌性蜘蛛中进行排斥操作的概率变小,进一步加强了局部搜索能力。动态概率因子PF如式(16)所示:
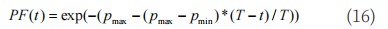
式中,pmax和pmin为自定义数值,具体取值如表2所示。改进后的概率因子取值如图1所示。
根据图1可以看出,本文的动态概率因子随迭代次数变化呈现动态递减状态。在算法计算过程中,迭代前期,较大的PF值使得雌性蜘蛛在位置更新过程中呈现较大概率的吸引操作,加快了算法的收敛速度。随着迭代次数的增加,蜘蛛种群的多样性降低,此时随着PF值动态减小,雌性蜘蛛在位置更新过程中增大排斥操作的概率。
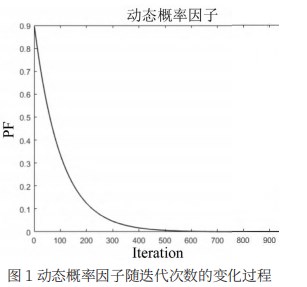
改进后的GSSO算法流程如图2所示。
3仿真实验与分析
将本文提出的GSSO算法与PSO算法、SSO算法、wDESSO[18]算法和ISSO[6]算法在同样条件下,通过选取适当的测试函数进行仿真试验,为了减小算法随机性对实验结果的干扰,对每个测试函数进行了多次独立运算,将测试函数的最优值、均值以及标准差作为函数性能评价指标。
3.1测试函数及参数设置
在30维情况下,将本文提出的GSSO算法、改进的wDESSO算法、SSO算法、PSO算法对表1中的10个测试函数进行了最小值寻优实验。实验中,蜘蛛的种群大小设为100,每次运行的终止迭代次数为1000。
在50维情况下,将本文提出的GSSO算法的测试结果与ISSO算法、wDESSO算法、SSO算法的测试结果进行对比。实验过程中的具体测试函数及参数设置参照文献[7]中的测试条件设定。
在30维测试实验中,GSSO算法、wDESSO算法,SSO算法、PSO算法中具体的参数设置如表2所示。
3.2实验结果与分析
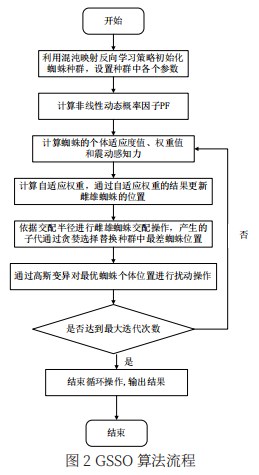
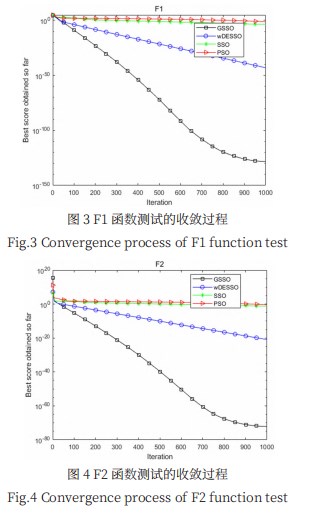
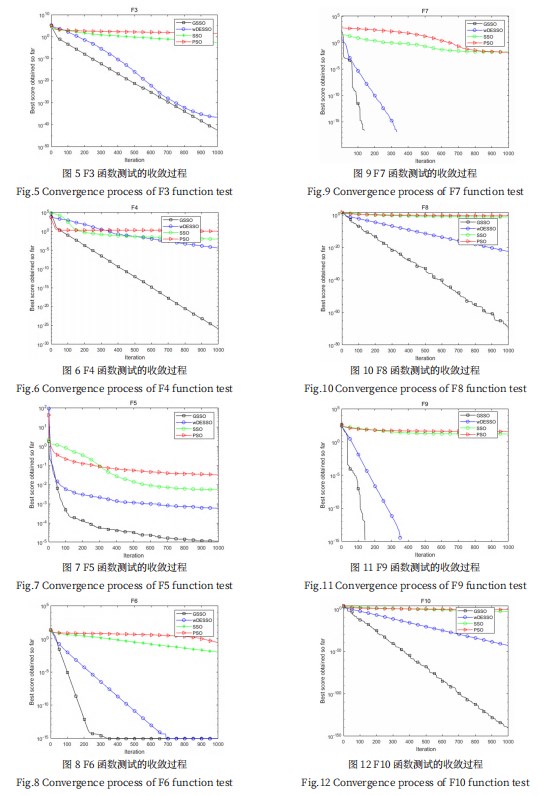
如图3—图12所示给出了30维情况下,GSSO算法与wDESSO算法、SSO算法、PSO算法对表1所示的10个测试函数的寻优收敛过程的曲线。
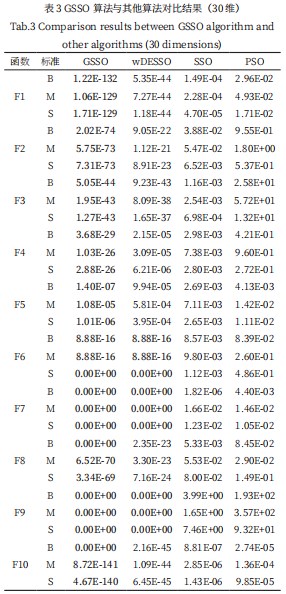
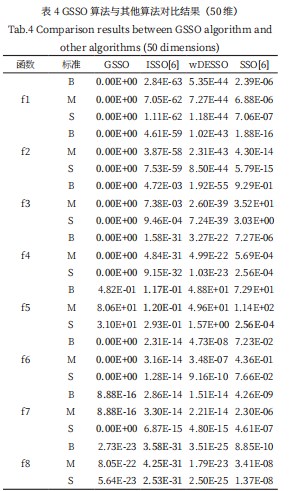
如表3所示给出前述四种算法针对最优值、均值以及标准差这三个性能指标的结果,其中,B代表最优值,M代表均值,S代表标准差,黑体表示对比试验中最优解。如表4所示为本文提出的GSSO算法与ISSO算法、wDESSO算法、SSO算法在50维情况下的实验结果,表中性能指标及黑体标注与表3相同。
由图3—图12中显示的针对不同函数测试的收敛过程对比图中可以看出:图3、图4、图5和图10、图12中的GSSO算法对于F1和F2函数的收敛精度明显高于其他三种算法;图5中wDESSO算法在迭代前期收敛速度加快,接近于GSSO算法,但在迭代后期wDESSO算法的收敛速度有所下降,其最终的最优值精确度不如GSSO算法;图7中,wDESSO算法、SSO算法、PSO算法均陷入局部最优值状态,GSSO算法则能够进行很好地收敛;图8中wDESSO算法最终的最优值精确度与GSSO算法相同,但GSSO算法在第237次迭代时就达到了最优收敛精度;图9、图11中GSSO算法和wDESSO算法均达到了理论最优精度,GSSO算法在收敛速度上优于wDESSO算法。
表3的数据显示GSSO算法在F7~F10函数测试中通过迭代实验均达到了理论最优收敛精度,具体为:GSSO算法在F1~F5函数测试中,最优值、均值以及标准差均优于wDESSO算法,相对于SSO算法,PSO算法,收敛精度有大幅度提高;在F6、F7、F9函数测试中GSSO算法和wDESSO算法具有相同的收敛精度,同时优于其他两种算法。
表4中的黑体标注显示GSSO算法整体性能优于其他的4种对比算法,具体为:在f1~f4和f6函数测试中,GSSO算法均能获得目标全局最优值,而ISSO算法、wDESSO算法、SSO算法均陷入了局部最优解的状态;而在f5函数测试中,ISSO算法的最优值及均值略小于GSSO算法,SSO算法的标准差优于GSSO算法;在f7函数测试中,GSSO算法陷入了局部最优解未能达到目标全局最优值,但最优值、均值以及标准差均优于其他对比算法,GSSO算法最终的收敛精度有显著地提高。在f8函数测试中,ISSO算法性能指标优于本文提出的GSSO算法。
通过以上分析看出,随着维度的增加,GSSO算法的收敛性能并没有下降,而且在50维的条件下,相对于30维有更多的测试函数达到了目标全局最优值。因此测试数据表明GSSO算法的性能随着维度的增加,仍能表现出良好的收敛能力,具有良好的适应性。
4结语
本文提出的混沌映射与高斯变异的群居蜘蛛优化算法首先是在wDESSO算法的基础上改进自适应权重的公式,在种群初始化过程中通过Logistic映射反向学习策略来均匀化种群分布状态;其次在雌性蜘蛛位置更新过程中对概率因子进行改进,采用动态概率因子来控制算法动态平衡局部和全局收索能力;最后,将wDESSO算法中的差分变异策略改进为高斯变异策略,并将其应用于交配后种群中最优个体位置的扰动,有效防止了算法在迭代后期易陷入局部最优值,提高了种群多样性,并提高了算法的收敛速度和求解精度。通过对多个测试函数进行仿真实验分析可以看出,改进后的GSSO算法在不同维度上,相较于wDESSO算法和ISSO算法,其收敛速度和收敛精度方面都有了较大的提升。在针对部分函数的寻优过程中仍然不能到达最优结果,后续研究过程中,对算法的寻优性能仍需要进一步提高。
参考文献
[1]CUEVAS E,CIENFUEGOS M,ZALDIVA D,et al.A Swarm Optimization Algorithm Inspired in the Behavior of the Social Spider[J].Expert System with Applications,2013,40(16):6374-6384.
[2]CUEVAS E,CIENFUEGOS M.A New Algorithm Inspired in the Behavior of the Social Spider for Constrained Optimization[J].Expert Systems with Applications,2014,41(2):412-425.
[3]BANKS A,VINCENT J,ANYAKOHA C.A Review of Particle Swarm Optimization.Part I:Background and Development[J].Natural Computing,2007,6(4):467-484.
[4]KARABOGA D,BASTURK B.A Powerful and Efficient Algorithm for Numerical Function Optimization:Artificial Bee Colony(ABC)algorithm[J].Journal of Global Optimization,2007,39(3):459-471.
[5]王丽,王晓凯.多峰函数优化的改进群居蜘蛛优化算法[J].计算机工程与应用,2017,53(3):1-6.
[6]YANG W,CHENG T,GUO Y,et al.A Modifified Social Spider Optimization for Economic Dispatch with Valve-Point Effffects[J].Complexity,2020.
[7]向蕾,鲁海燕,胡士娟,等.改进的基于差分进化的群集蜘蛛优化算法[J].传感器与微系统,2021,40(06):121-125+132.
[8]张晓桐.基于智能算法的异构网络资源分配[D].哈尔冰:哈尔滨工程大学,2019.
[9]李杨,战艺,李岩舟.基于改进蜘蛛群居算法的移动机器人路径规划方法研究[J].科学技术与工程,2016,16(35):225-230.[10]WANG Y J,LI X J,XIAO J.Social Spider Optimization with Dynamic Learning Strategy[J].Control and Decision,2015(09):1575-1582.
[11]SUN S C,QI H,REN Y T,et al.Improved Social Spider Optimization Algorithms for Solving Inverse Radiation and Coupled Radiation-conduction Heat Transfer Problems[J].International Communications in Heat and Mass Transfer,2017,87:132-146.
[12]TAMILARASI K,GOGULKUMAR M,VELUSAMY K.Enhancing the Performance of Social Spider Optimization with Neighbourhood Attraction Algorithm[J].Journal of Physics ConferenceSeries,2021,1767(1):12-17.
[13]肖素琼,罗可.具备反向学习和局部学习能力的磷虾群算法[J].计算机工程与应用,2018,54(18):34-39.
[14]王涛,Ryad Chellali.非线性权重和收敛因子的鲸鱼算法[J].微电子学与计算机,2019,6(1):11-15.
[15]张晓莉,王秦飞,冀汶莉.一种改进的自适应惯性权重的粒子群算法[J].微电子学与计算机,2019,36(3):66-70.
[16]YU L I,PEI Y H,LIUJ S.Bat OptimalAlgorithm Combined Uniform Mutation with Gaussian Mutation[J].Control and Decision,2017,32(10):1775-1781.
[17]高文欣,刘升,肖子雅,等.柯西变异和自适应权重优化的蝴蝶算法[J].计算机工程与应用,2020,56(15):43-50.
[18]QIU J F,XIE J,CHENG F,et al.A Hybrid Social Spider Optimization Algorithm with Differential Evolution for Global Optimization[J].Journal of Universal Computer Science,2017,23(7):619-635.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/41043.html