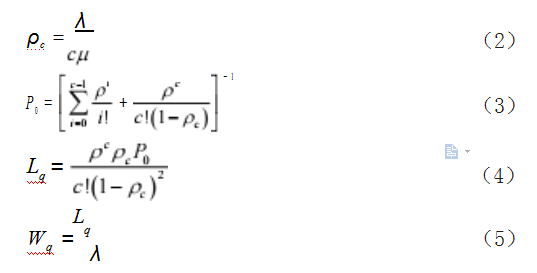SCI论文(www.lunwensci.com)
摘 要:为了提高 Modelica 云仿真系统任务调度的均衡性和效率,同时最大化资源提供者的利益,构建基于排队理论的 云仿真技术任务调度系统模型,考虑等待队列长度和仿真系统的模块分配,结合排队理论分析任务调度策略,提出 Modelica 云仿真系统模块化的 M/M/c 串联排队模型方案。实验结果表明,与传统的单一 M/M/c 模型相比, M/M/c 串联排队模型在相同 成本指标下更能满足资源提供者对于系统效率的需求。
关键词:仿真任务调度 ;排队论 ;云仿真 ;Modelica
Research on Modelica Cloud Simulation Resource Scheduling System Planning Based on Queuing Theory
WU Weiwei1, LIU Huijuan1,2, LIU Jian1,2, ZHOU Runze1
(1.Institute of Intelligent Control Technology, XCMG Research Institute, Xuzhou Jiangsu 221004;2.State Key
Laboratory of Intelligent Manufacturing of High end Construction Machinery of XCMG, Xuzhou Jiangsu 221004)
【Abstract】:In order to improve the balance and efficiency of task scheduling of Modelica cloud simulation system and maximize the interests of resource providers, a cloud simulation technology task scheduling system model based on queuing theory is constructed, considering the waiting queue length and module allocation of the simulation system, the task scheduling strategy is analyzed in combination with queuing theory, a modular M/M/c series queuing model scheme for Modelica cloud simulation system is proposed. The experiment results show that: Compared with the traditional single M/M/c model, the M/M/c series queuing model can better meet the needs of resource providers for system efficiency under the same cost index.
【Key words】:simulation resource scheduling system;queuing theory;cloud simulation;Modelica
0 引言
近年来,建模仿真系统日益复杂化, Modelica 单机 多领域建模工具已经不能支撑知识共享、分布式建模以 及联合仿真的工作,迫切需要能支撑分布式协作的多领 域建模仿真平台。而云计算作为一种新型的超级计算方 式,被引入到Modelica 多领域仿真任务优化求解效率 的问题,为海量仿真任务的建模和仿真提供了新的解决 思路 [1]。目前,大量的文献提供了云计算系统中资源分 配的策略 [2]。而对于云仿真系统,如何在满足系统性能需求的基础上降低整个仿真系统的运行成本,又成为研 究的新的问题 [3-4]。因此,为了获得快速理想以及高效费 比的建模仿真计算结果,本文提出了一种适用于大规模 多任务的基于 Modelica 云仿真任务调度系统的排队模型。
1 Modelica 云仿真任务调度系统的排队模型设计
1.1 系统概述
Modelica 仿真任务调度系统主要包含运行于后端 的 Modelica 标准模型生成过程、编译过程和求解过程 三部分,用于实现仿真模型计算的全过程任务调度与处理。Modelica 模型生成过程、编译过程和求解过程三 个环节相互独立,前端将构建好的模型关键信息传输至 后端,提交至图文转换队列中,接着后端的仿真任务调 度系统分配仿真任务至各个图文转换节点中,将模型关 键信息转换为 Modelica 标准模型,并将编译请求提交 至模型编译队列中,仿真任务调度系统分配编译任务 至各个编译节点中,并将求解请求提交至模型求解队列 中,仿真任务调度系统分配求解任务至各个求解节点 中,求解数学模型得到仿真结果。
1.2 排队模型概述及初步设计
一般排队模型包括顾客流、排队结构、服务机构三 部分。排队论通过对顾客流的到达时间和服务机构的服 务时间等数据进行统计研究,重新规划服务系统结构, 使系统在不同需求下达到当前需求的最优解。依据排队 论建立 Modelica 云仿真过程中任务调度资源分配的排 队模型,并给定约束 :
(1)请求仿真的模型数量无上限,并假定各模型到 达的时间相互独立且服从同一负指数分布,单位时间内 进入系统的模型数服从泊松分布。(2)整个系统中计算 节点的服务率相等,并假定各类型的服务机构服务率服 从泊松分布。(3)所有环节的顾客流均服从先到先服务 的服务规则 :
其中, ρ 表示单个系统服务的利用率, λ 表示单位 时间平均到达的请求数量, μ 表示单位时间平均完成的 服务数量。
遵循以上约束条件,参照单机版仿真节点,根据单 队列多服务台排队模型(1 个 M/M/c 模型),设计仿真 任务调度系统,其中顾客流为仿真任务组,顾客为仿真 任务,服务台为各环节的计算节点,输出仿真结果视为 服务完成,整个模型仅有 1 个队列,其排队模型可视为 M/M/c 队列模型 :此时系统服务强度 ρc,系统中所有 服务台均闲置的概率 P0,平均队长 Lq,货物平均等待 时间 Wq,系统内货物必须排队的概率 P(N ≥ c),服务 台运行效率 θ 为 :
1.3 优化排队模型
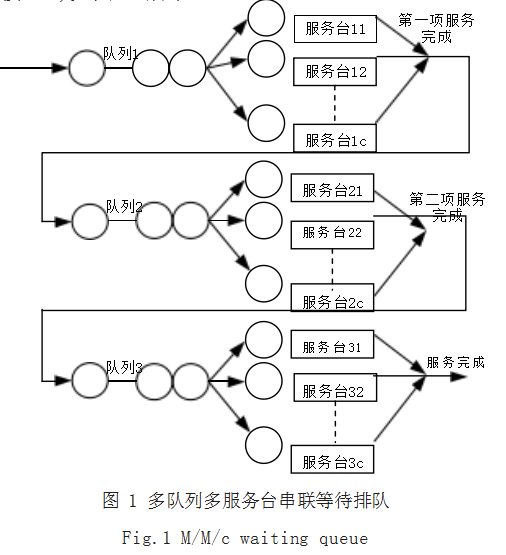
鉴于 Modelica 云仿真任务调度系统的各个环节可 以相互独立运行且运行效率存在差异性,将具体排队模 型优化为多队列多服务台分解排队模型(即 M/M/c 串 联模型),如图 1 所示 :
整个模型具有 3 个队列,根据 Burke 定理,对于在 平衡状态时的 M/M/c 系统,服务完成的瞬间的序列服从 和输入过程具有相同的参数,因此可视为 3 个 M/M/c 模 型串联。根据排队论对 Modelica 云仿真任务调度系统 的各个环节进行建模 :(1)Modelica 标准模型生成过 程中,顾客流为模型关键信息,服务台为图文转化节点, 以下统称为计算节点,生成 Modelica 标准模型即视为 服务结束。(2)编译过程中,顾客流为 Modelica 标准 模型,服务台模型编译节点,以下统称为计算节点,生 成平坦化混合数学模型即视为服务结束。(3)求解过程 中,顾客流为平坦化混合数学模型,服务台为模型求解 节点,以下统称为计算节点,求解模型得到仿真结果即 视为服务结束。
2 Modelica 云仿真调度系统的排队模型求解任务分析
2.1 根据需求计算节点的仿真任务量
根据 A 公司单机版建模统计实际需求量,推算出云 平台总体仿真任务量,涉及的主要参数为 :任务统计天 数 N,任务平均到达率 λ ;节点平均计算率 μ。两周任 务平均到达数量统计如表 1 所示。
表 1 两周任务平均到达数量统计
Tab.1 Statistics of average arrival quantity of tasks in twoweeks
| 时间 |
N |
均值 |
标准差 |
| 8:30-10:30 |
10 |
11019 |
6.229 |
| 10: |
30-12:30 |
10 |
18556 |
11.883 |
| 13: |
30-15:30 |
10 |
13715 |
8.485 |
| 15: |
30-17:30 |
10 |
6657 |
11.679 |
经样本假设检验,实际样本服从参数为 λ 的泊松分 布。经计算, λ=6243.375 个 / 小时。两周任务各计算节 点平均计算时间统计如表 2 所示。
表 2 两周任务各计算节点平均计算时间统计(N=10)
Tab.2 Statistics of average calculation time of eachcalculation node of two-week task(N=10)
| 时间 |
均值 1 |
标准差 1 |
均值 2 |
标准差 2 |
均值 3 |
标准差 3 |
| 8:30-10:30 |
11.421 |
8.233 |
54.769 |
11.387 |
6.016 |
10.387 |
| 10: |
30-12:30 |
13.768 |
10.583 |
67.326 |
12.285 |
6.744 |
10.924 |
| 13: |
30-15:30 |
10.643 |
12.011 |
55.137 |
9.447 |
5.687 |
6.832 |
| 15: |
30-17:30 |
16.716 |
9.592 |
79.473 |
10.391 |
8.112 |
7.485 |
经计算,三类节点的平均计算时间分别为 6.561s/ 个,32.088s/ 个,3.320s/ 个 ;μ1=548.697 个 / 小时, μ2= 112.191 个 / 小时,μ3=1084.378 个 / 小时。
2.2 各环节排队模型输入参数确定
(1)Modelica 标准模型生成环节 :模型生成能力 μ1 为大约 548.699 个 / 小时,已知模型关键信息即总体 仿真任务量, λ=6243.375 个 / 小时。根据以上参数,可 以得到系统服务强度 :ρ1=λ/μ1=11.379。故模型生成环 节计算节点的数量需要大于等于 12 个。(2)编译环节 : 模型编译能力 μ2 为大约 112.191 个 / 小时, 已知模型 关键信息即总体仿真任务量, λ=6243.375 个 / 小时。根 据以上参数,可以得到系统服务强度 :ρ2=λ/μ2=55.650。 故编译环节计算节点的数量需要大于等于 56 个。(3)求 解环节 :模型求解能力 μ3 为大约 1084.378 个 / 小时, 已知模型关键信息即总体仿真任务量, λ=6243.375 个 / 小时。根据以上参数,可以得到系统服务强度 :ρ3=λ/ μ3=5.758。故求解环节计算节点的数量需要大于等于 6 个。
3 仿真分析
本文描述的 Modelica 云仿真任务调度系统,其运 维成本主要包含后端模型生成节点、编译节点、求解节 点的部署成本及其对应的运维成本,三种节点的部署和 运维成本几乎一致。M/M/c 串联方案计算节点总数为三个环节计算节点数之和 77,与 M/M/c 方案计算节点 25/26 时成本基本一致, 但此时 ρc>1, 队长无限增加, 无法满足系统仿真性能需求。参照式(1)~ 式(8)的 计算过程,可以得出计算 M/M/c 方案需要的服务台数 为 72.786, 下面分别对于任务数目为分别选取服务台 计算点数为 73 或 74,比较此时 3 个 M/M/c 串联与 M/ M/c 两种方案,如表 3 所示。
表 3 M/M/c 串联与 M/M/c 排队参数列表
Tab.3 M/M/c Series and M/M/c queuing parameter list
| M/M/c |
M/M/c 串联 |
| 名称 |
73 |
74 |
77 |
| 所有服务台闲置概率 |
1.50×10-33 |
7.357×10-33 |
9.756×10-6 |
| 平均队长 |
328.710 |
50.197 |
39.223 |
| 平均等待时间 |
189.538s |
122.982s |
22.617s |
| 排队概率 |
0.970 |
0.838 |
0.958 |
| 运行效率 |
0.997 |
0.983 |
0.813 |
选择 3/M/M/c 方案参数总的参数列表为 :
总平均队长 :
L =3.857 + 32.889 + 2.477 = 39.223
任务平均等待时间 :
W =2.224+ 18.965 + 1.428 = 22.617s
任务必须排队效率 :
P=1-(1-0.550)×(1-0.798)×(1-0.534)=0.958
3 个 M/M/c 串联方案平均队长相比 M/M/c 减少了 21.9%, 任务平均等待时间相比 M/M/c 减少了 81.6%, 成本相比 M/M/c 减少了 65.3%。
4 结语
本文提出了一种基于排队理论规划 Modelica 云仿 真任务调度系统的方法,并针对系统的模型生成、编 译和求解三个环节进行分别分析。选择排队论数学建模 M/M/c 串联方案,通过仿真验证了 M/M/c 串联排队模 型理论运用在该系统的优越性。
参考文献
[1] 全力,傅明.云计算中任务调度优化策略的研究[J].计算机工 程,2018,44(8):14-18.
[2] 蒙殿元.一个多服务台系统和多个单服务台系统工作效率的 比较[J].海峡科学,2011(11):32-33.
[3] 吴义忠,吴民峰,陈立平.基于Modelica语言的复杂机械系统 统一建模平台研究[J].中国机械工程,2006(22):2391-2396.
[4] 吴义忠,蒋占四,丁建完,等.多领域仿真模型分治求解策略 [J].华中科技大学学报(自然科学版),2008(10):41-44.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/38040.html