SCI论文(www.lunwensci.com):
摘 要:为了优化图拉普拉斯矩阵和字典学习建立图像恢复模型,该模型目标函数包括数据保真项、图拉普拉斯正则化项 和稀疏表示项,本文提出基于变量分离的拉格朗日优化算法,该算法通过归一化图拉普拉斯矩阵的特征向量作为系数编码的初 始字典,不断迭代学习算法逐渐优化先验信息、字典、稀疏系数。实验结果表明,该算法具有可行性和有效性,在定量评价和 视觉感知效果方面优于传统方法。
关键词: 图拉普拉斯矩阵 ;字典学习 ;拉格朗日方法 ;变量分离 ;正则化
Lagrangian Optimization Algorithm of Variables Splitting for Image Denoising
SHANG Lijuan, GUO Pengfei
(Guangdong Neusoft University, Foshan Guangdong 528225)
【Abstract】: To optimize a graph Laplacian matrix term and dictionary learning term for our return model, which the objective function consists of a data fidelity term, a graph Laplacian regularizer term and a sparse representation term, we propose a Lagrangian algorithm based variables splitting. We choose the eigenvectors of the normalized graph Laplacian matrix as an initial dictionary for the sparse coding, and continuous iterative learning algorithm gradually optimizes prior information, dictionary, sparse coefficient. Experimental results demonstrate that the proposed model is feasible and effective, as the same time outperforms traditional method, in terms of both objective measurements and perceptual quality.
【Key words】: graph laplacian matrix;dictionary learning;lagrangian method;variables splitting;regularizer
0 引言
由于电子设备、传输信道和其他环境因素影响,图像 在采集、压缩和传输的过程中受到不同程度噪声污染,无 法清晰观测图像细节信息,因此,图像降噪具有重要理论 研究价值和现实意义
[1-2],它需要从含有加性高斯白噪声 (Additive White Gaussian Noise, AWGN) N ∈ R
M×N 的 观察信号 Y ∈ R
M×N 中估计原始信号 X ∈ R
M×N,加性噪声模型可表示为
Y=X+N (1)
本文针对非凸性的降噪模型提出一种优化求解算法,通过基于变量分离的拉格朗日算法获得最优解。
1 相关工作
1.1 基于字典学习的稀疏表示
早期的稀疏表示选取一个正交基作为稀疏基,然后 将信号在该正交基上展开从而得到信号在该正交基下 的稀疏表示,正交变换空间的稀疏表示操作简单、效 率高,不足在于灵活性差,利用冗余字典学习表示信号 比使用固定基(如傅里叶变换、小波变换 [3])更好,因 此,基于字典学习的稀疏表示方法成为研究热点。给出 字典 D ∈ R
m×n,观测信号 y ∈ R
m 稀疏表示模型为
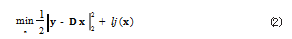
字典 D 包含 n 个原子,每个原子有 m 个特征点。 理想信号 x ∈ R
n, φ 是稀疏表示函数,例如 l
0 范数、l
1 范数和全变差(Total Variation, TV) 范数 [4]。正则化 参数 λ 权衡保真项和稀疏表示先验项。稀疏表示的目的 是对于给定一个字典 D 求系数 x。
1.2 图拉普拉斯矩阵
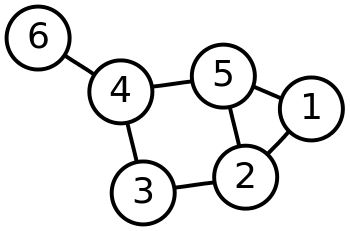
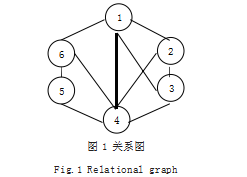
图拉普拉斯算法已经运用到降维、聚类、半监督学 习和图像处理中。图像像素点之间具有相关性,可以表示为拥有 n 个节点的关系图,如图 1 所示,它的拉普拉 斯矩阵 L ∈ R
n×n 定义为
其中P∈R
n×n 表示图的度矩阵,A ∈ {0,1}
n×n 表示 图的邻接矩阵,其元素表示对应顶点是否连通。对角矩阵 P 包含了每个顶点的度信息,也就是顶点所连通的边数。
2 图像降噪模型
图像降噪是欠定问题,求解过程引入图像先验信息 至关重要。利用图拉普拉斯可以捕捉邻近像素点的关联 性这一特性,引入图拉普拉斯正则化项,同时引入关联 稀疏系数与字典的约束项从而保证用字典 D 稀疏表示 原信号 x。则图像降噪模型表示为
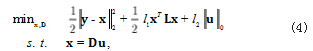
其中 L 是归一化后的图拉普拉斯矩阵,u 是稀疏系数。该模型包含了数据保真项、图拉普拉斯正则化项和 稀疏表示项。数据保真项确保原图和降噪后图像的相似 性,图拉普拉斯正则化项描述邻近像素之间的关联性, 稀疏表示项由字典关联稀疏系数与理想信号 x 进行约束。正则化参数 λ
1 和 λ
2 分别权衡图拉普拉斯正则化项 和稀疏表示项。
本模型不同于传统的模型,因使用稀疏项‖
u ‖
0 代 替‖
x‖
0 而引入一个等式约束,对于这一含有等式约束的 优化问题,本文提出基于变量分离的拉格朗日优化算法。
3 本文算法
本文提出一种基于变量分离的拉格朗日的迭代算法 以求解公式 (4) 中图像降噪模型,以规范化图拉普拉斯矩阵的特征向量作为初始字典 D(0)。通过不断迭代优化 先验信息、字典及稀疏系数。算法的关键步骤包括 :块 匹配,估计图拉普拉斯矩阵 L,基于拉格朗日增广方程 的稀疏编码和字典学习。
3.1 块匹配和总梯度计算
给出噪声图像块 p0 ∈ R

×
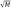
,可以在一定的窗口内利用欧式距离找出 K-1 个与它相似的块,把第 k 个相 似块拉直成列向量 pk ∈ R
M(k=0,1,...,K-1), 这个集合称 作一类,每一列
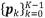
都有它在原图中相应图像块的坐 标索引。对于类

∈ RM×K,先把每一列转换成块

,然后计算水平梯度和垂直梯度
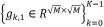
。每个梯度块拉直成一列, 再组成矩阵 h
1 ∈ R
M×K 和 h
2 ∈ R
M×K,总的梯度 h 由 h
1 和 h
2 组成,即 h=[h
1;h
2] ∈ R
2M×K。
3.2 计算图拉普拉斯矩阵 L
对当前像素点 i 的 K 个相似块,其对应总梯度为 h,用 ω
ij(j=1,2,...,K-1) 表示邻接矩阵 A 的元素,即 A(i,j)=ω
ij, ω
ij 计算公式为
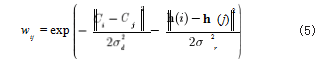
I × L 是欧式距离,C
i,C
j 表示当前第 i,第 j 像素点 的坐标,h(i),h(j) 表示 h 的第 i, 第j 列。σd 和 σr 表 示在灰度和空域中控制权重下降参数。
归一化拉普拉斯矩阵 L 可以分解为 L=QΛQ
T,选取 特征向量作为稀疏编码字典学习的初始字典 D
(0)=Q
T。
3.3 基于变量分离的拉格朗日优化算法
为求解模型 (4),在 x=Du 约束下利用先验信息 x 更 新字典,使训练字典更加完备,建立拉格朗日增广方程
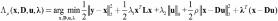
ρ>0 为权重参数, λ 是一个和等式约束关联的矢量。 求解公式 (6) 时,x,D,u,λ4 个变量中,利用控制变量法 逐渐迭代更新每一个参数,更新方法如下 :
更新 x :利用公式 (6) 对 x 求导,得 :
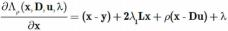
令∇x Λρ (x,D,u,λ)=0,得 :

更新 D :公式 (6) 对 D 求导,得 :

= - rxuT + rDuuT - λuT
令∇D Λρ (x,D,u,λ)=0,得 :
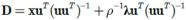
更新 u :公式 (6) 不能对 u 直接求导,因为 l
0 范数 不可导,可采用梯度下降法和硬阈值迭代法更新 u。先 对光滑部分求偏导,即 :

梯度下降法表示为
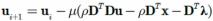
硬阈值收缩步
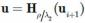
更新 λ :
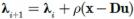
通过循环迭代对每一噪声图像块进行更新,可得到 相应的清晰图像块 x。
3.4 降噪图像估计
对每个像素点,均得到一个降噪图像块,一个像素 点位于不同的块中,因此最终每个像素点的灰度值即是 这些重叠块的平均值,于是得到降噪后的图像 X*。
4 实验与分析
在实验中,设置参数为正则化系数 λ
1=0.01, λ
2=0.05, ρ=50,μ=1.5, 块大小
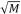
×
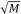
为 7×7,最大迭代次数 为 5,相似块数目 K=32。为验证本文所提图像降噪算法 性能,向选取图像中分别加入均值为 0,标准方差为 10、 20、30、50 的加性高斯白噪声,利用所提算法进行降噪 处理, 并将结果与传统 NLM、K-SVD、BM3D 算法进 行比较,得到一组边缘清晰,纹理保留较丰富的高质量图像。
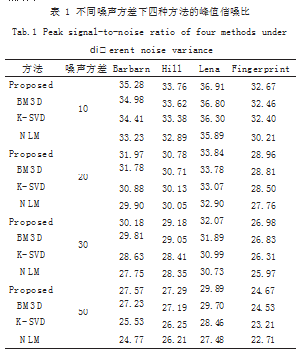
本文提出的方法在效果上优于传统方法,能够保留 更多的纹理细节信息,避免产生伪影,尤其是在图像边 缘区域,既可以增强边缘对比,又能有效提升区域亮度比和增强亮度梯度信息。为了定量分析本文算法有效性, 我们使用峰值信噪比 (PSNR) 和结构相似度 (SSIM) 作为 恢复图像质量的评价标准 , 表 1 为不同噪声方差下四种 方法针对不同图片得到的 PSNR 值和 SSIM 值, 由表 1 可知,本文算法优于传统图像降噪算法,得到较好的降 噪效果。
5 结语
本文针对将图拉普拉斯项和字典学习表示约束项作 为先验因子的图像降噪模型提出一种新的求解算法。用 归一化的图拉普拉斯矩阵特征向量作为初始字典,利用 变量分离拉格朗日优化算法优化稀疏编码和字典学习, 为后续将该算法扩展应用到其他图像处理和机器学习优 化问题中奠定基础。
参考文献
[1] Fan L,Zhang F,Fan H,et al.Briefreview ofimage denoising techniques[J].Visual Computing for Industry,Biomedicine, and Art,2019,2(1):7.
[2] Romano Y and Elad M.Boosting of image denoising algorithms[J].SIAM Journal on Imaging Sciences,2015,8(2): 1187-1219.
[3] Shuman D I,Wiesmeyr C,Holighaus N,et al. Spectrum- adapted tight graph wavelet and vertex-frequency frames[J].IEEETransactionsonSignalProcessing,2015,63(16):4223-4235.
[4] Rudin L I,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica D:Nonlinear Phenomena,1992,60(1):259-268.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/35818.html

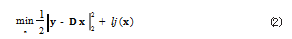

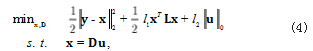
 ×
× 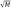 ,可以在一定的窗口内利用欧式距离找出 K-1 个与它相似的块,把第 k 个相 似块拉直成列向量 pk ∈ RM(k=0,1,...,K-1), 这个集合称 作一类,每一列
,可以在一定的窗口内利用欧式距离找出 K-1 个与它相似的块,把第 k 个相 似块拉直成列向量 pk ∈ RM(k=0,1,...,K-1), 这个集合称 作一类,每一列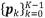 都有它在原图中相应图像块的坐 标索引。对于类
都有它在原图中相应图像块的坐 标索引。对于类 ∈ RM×K,先把每一列转换成块
∈ RM×K,先把每一列转换成块 ,然后计算水平梯度和垂直梯度
,然后计算水平梯度和垂直梯度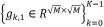 。每个梯度块拉直成一列, 再组成矩阵 h1 ∈ RM×K 和 h2 ∈ RM×K,总的梯度 h 由 h1 和 h2 组成,即 h=[h1;h2] ∈ R2M×K。
。每个梯度块拉直成一列, 再组成矩阵 h1 ∈ RM×K 和 h2 ∈ RM×K,总的梯度 h 由 h1 和 h2 组成,即 h=[h1;h2] ∈ R2M×K。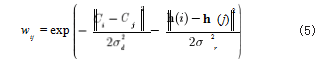
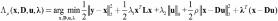
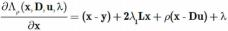

 = - rxuT + rDuuT - λuT
= - rxuT + rDuuT - λuT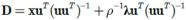

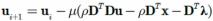
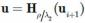
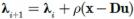
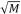 ×
×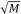 为 7×7,最大迭代次数 为 5,相似块数目 K=32。为验证本文所提图像降噪算法 性能,向选取图像中分别加入均值为 0,标准方差为 10、 20、30、50 的加性高斯白噪声,利用所提算法进行降噪 处理, 并将结果与传统 NLM、K-SVD、BM3D 算法进 行比较,得到一组边缘清晰,纹理保留较丰富的高质量图像。
为 7×7,最大迭代次数 为 5,相似块数目 K=32。为验证本文所提图像降噪算法 性能,向选取图像中分别加入均值为 0,标准方差为 10、 20、30、50 的加性高斯白噪声,利用所提算法进行降噪 处理, 并将结果与传统 NLM、K-SVD、BM3D 算法进 行比较,得到一组边缘清晰,纹理保留较丰富的高质量图像。