一种基于干涉测角衰减记忆 Kalman 算法的仿真应用论文

SCI论文（www.lunwensci.com）:
 
摘   要：本文结合干涉仪测角 Kalman 滤波算法、衰减记忆 Kalman 滤波算法，实际应用时，由于模型与实际过程可能 不符，此时新息对估计值的修正作用下降，导致卡尔曼滤波发散。增大新息对估计值的权重，是扼制滤波发散的一个可行途 径。本文对比 Kalman 滤波算法、衰减记忆 Kalman 滤波算法仿真分析，并给出了仿真结果，由仿真结果可知，在一定通道 相位噪声的条件下，对于正弦运动，采用衰减记忆以后，卡尔曼滤波结果得到了明显的改善，角度角速度误差均明显减小。增 大新信的比重，同时监控算法是否发散，可以明显改善滤波效果。

关键词：卡尔曼滤波 ；衰减记忆 ；解模糊
         【Abstract】： This paper combines interferometer angle measurement and Kalman filtering algorithm,fading- memory Kalman filtering algorithm. In practical application, due to the possible inconsistency between the model and the actual process, the correction effect of innovation on the estimated value decreases, resulting in the divergence of Kalman filter. Increasing the weight of innovation to the estimated value is a feasible way to curb the filter divergence. This paper compares the simulation analysis of Kalman filtering algorithm and fading-memory Kalman filtering algorithm, and gives the simulation results. The simulation results show that under the condition of certain channel phase noise, the Kalman filter results are significantly improved for sinusoidal motionafter using fading-memory, the angular and angular velocity errors are significantly reduced. Increasing the proportion of new signals and monitoring whether the algorithm is divergent can significantly improve the filtering effect.
        【Key words】： Kalman filtering;fading-memory; unwrap ambiguity

0 引言

         由平行波干涉测角算法、几何对消干涉测角算法等 干涉仪测角算法得到测量角度后，利用 Kalman 滤波 能够进一步降低测量误差，并且能够得到角度、角速度 等测量结果。但是在实际应用中，由于系统噪声、观测 噪声、实际运动模型难以准确描述，尤其是在滤波数学 模型与实际过程的数学规律不匹配时 , 会使滤波精度下 降 , 严重时会导致滤波发散 , 本文介绍一种基于干涉测 角衰减记忆 Kalman 算法，并给出仿真数据。

1 角度测量 Kalman 滤波

卡尔曼滤波器模型如下 ：

        假设 n 时刻目标航天器相对于追踪航天器的俯仰角为θn，角速度为θn，角加速度θn，时间间隔为∆T ，按照匀加速模型，系统的状态方程为 ：



是零均值的白噪声矢量，状态噪声矩阵Q = E {Mn  ⋅ M T n }。
卡尔曼滤波方程如下 ：



        实际应用时， 由于模型与实际过程可能不符，此时 新息对估计值的修正作用下降，导致卡尔曼滤波发散。 因此增大新息对估计值的权重，是扼制滤波发散的一个 可行途径。

        衰减记忆卡尔曼滤波方程与上述卡尔曼滤波方程基 本相同，仅对（3）式修正如下 ：
Pn|n−1  = F (Pn−1|n−1 ⋅ g )FT  +ΓQn−1ΓT

        式中，衰减因子 g 是一个大于 1 的标量因子，其取 值依据角加速度（反映了动态）而定，角加速度越大， 衰减因子越大。同时采用滤波前角度的差分（微分）可 以得到角速度监控算法是否发散。

2 仿真分析

        对角度进行卡尔曼滤波可以得到角度和角速度测量 值 ；采用衰减记忆卡尔曼滤波也可得到角度、角速度 测量值，下面比较这两种算法。仿真中采用根据距离 和角加加速度实时估计观测噪声、系统噪声，仿真中 ∆T = 4ms。当运动模型不是匀加速模型时，采用衰减记 忆卡尔曼滤波算法后滤波结果得到改善。下面在角度运 动模型为正弦运动时，比较这两种算法的滤波结果。

       仿真设置 ：仿真时间为 500s，初始距离为 80Km， 初始速度为 100 m/s，初始角度 -30°，正弦周期为 60s， 噪声为零均值高斯白噪声，其标准差为 0.1°。

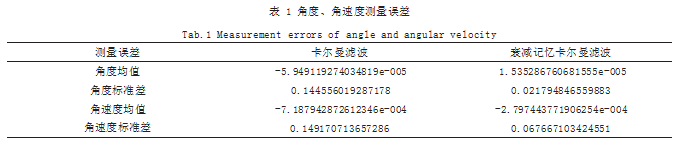
       仿真结果 ：卡尔曼滤波与衰减记忆卡尔曼滤波后角 度、角速度测量误差的均值和标准差如表 1 所示 ：
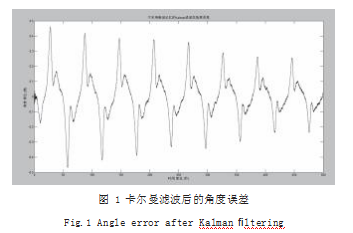
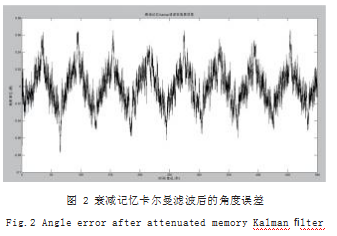
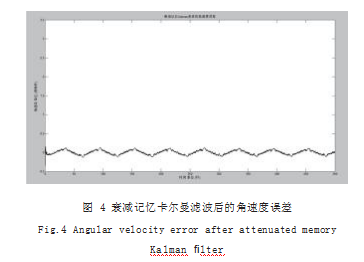
仿真结果图如图 1 至图 4 所示，分别是卡尔曼滤波后的角度误差、衰减记忆卡尔曼滤波后的角度误差、卡
尔曼滤波后的角速度误差和衰减记忆卡尔曼滤波后的角速度误差。

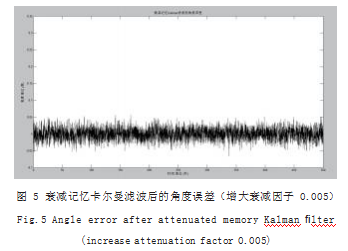
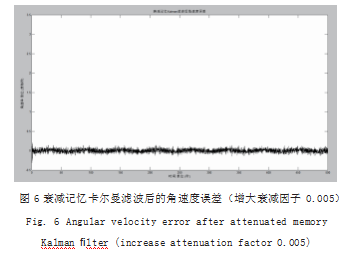
         由以上仿真可知，对于正弦运动模型，采用衰减记忆以后，卡尔曼滤波结果得到了明显的改善，角度角速度误差均明显减小。但是，也可以分析发现，角度和角速度误差也具有周期性，周期与角度运动周期相当，说明仍需调整衰减因子，增大新信的比重。将衰减因子提高 0.005，其他条件不变，仿真结果如图 5、图 6 所示，可以看出效果得到改善 ：

3 结论

       本文结合干涉仪测角与 Kalman 滤波算法、衰减记忆 Kalman 滤波算法，实际应用时，由于模型与实际过程可 能不符，此时新息对估计值的修正作用下降，导致卡尔曼 滤波发散。因此增大新息对估计值的权重，是扼制滤波发 散的一个可行途径。本文对比 Kalman 滤波算法、衰减记 忆 Kalman 滤波算法仿真分析，并给出了仿真结果，由仿 真结果可知，在一定通道相位噪声的条件下，在角度运动 模型为非匀加速运动时，对于正弦运动，采用衰减记忆以 后，卡尔曼滤波结果得到了明显的改善，角度角速度误差 均明显减小。增大新信的比重，同时监控算法是否发散， 可以明显改善滤波效果。

参考文献

[1] 徐景硕,秦永元,彭蓉.自适应卡尔曼滤波器渐消因子选取方 法研究[J].系统工程与电子技术,2004(11):1552-1554.
[2] 杨春玲,倪晋麟,刘国岁,等.转换坐标卡尔曼滤波器的雷达目 标跟踪[J].电子学报,1999(3):121-123.
[3] 周前祥,连顺国.空间交会对接技术及其发展趋势[J].中国航 天,1998(1):25-28.
[4] Wigbert Fehse.Automated rendezvous and docking of spacecraft[M].New York:Cambridge Univeristy Press, 2003.
[5] 王一凡.空间交会对接光学敏感器测量的实验研究[J].航天 控制,1996(2):57-62.
[6] 张建军,邓琪,韩明,等.一种基于干涉测角Kalman算法的仿 真应用[A].天津市电子学会、天津市仪器仪表学会.第三十五届 中国(天津)2021’IT、网络、信息技术、电子、仪器仪表创新 学术会议论文集[C].天津市电子学会、天津市仪器仪表学会: 天津市电子学会,2021:4.
[7] 张建军,邓琪,韩明,等.一种平行波干涉测角算法及仿真[A]. 天津市电子学会、天津市仪器仪表学会.第三十五届中国(天 津)2021’IT、网络、信息技术、电子、仪器仪表创新学术会 议论文集[C].天津市电子学会、天津市仪器仪表学会:天津市 电子学会,2021:4.

 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jisuanjilunwen/35261.html