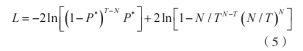[摘要]2023年以来,由ChatGPT及其他主要语言模型所带动的人工智能领域的热度,促进了美国股市的强劲上升,其中纳斯达克指数(以下称纳指)的表现格外突出。但金融市场环境复杂多变,拥有高收益的同时也要注意到其潜在的风险,因此,有效预测金融资产的在险价值(Value at Risk,VaR)具有非常重大的意义。文章通过运用MATLAB和EViews工具对纳指交易型开放式指数基金(Exchange Traded Fund,ETF)进行实证研究,发现其累计净值遵循几何布朗运动,且蒙特卡洛模拟能够较好地对该基金的累计净值进行价值估算。
[关键词]纳指ETF,VaR,蒙特卡洛模拟
0引言
VaR自20世纪90年代被提出以来,已成为金融行业评估风险的核心工具。VaR通过概率视角来评估投资组合潜在的最大亏损,根据现实操作经验,VaR的实施已经获得显著成效[1]。估算VaR可采用多种方法,包括方差-协方差法、历史模拟法和蒙特卡洛模拟法等。其中,方差-协方差法通常假定收益率遵循正态分布规律,但实际上金融市场的收益率分布往往呈现出厚尾特性,这可能导致对风险的低估。历史模拟法的一个核心假设是过去的市场情况会在未来重现,但这忽略了市场结构和动态可能随时间而改变的事实。而蒙特卡洛模拟因其灵活性和适应性常被认为是一种更全面的方式,尤其是在处理复杂金融产品和捕捉市场极端行为时有着非常不错的处理能力,并能提供较为精确的估算结果。因此,本文选择蒙特卡洛模拟法来计算纳指ETF的VaR值。
1 VaR概述
VaR衡量的是在常规市场波动条件下,特定的金融资产或投资组合所能承受的潜在最大损失。具体来说,它描述了在给定的显著性水平上,金融资产或证券组合在将来一段特定时间内可能遭受的最大损失量[2]。该概念通过数学公式表述为
式(1)中,P代表资产价值低于潜在最高损失界限的可能性,∆P指在特定持有期间∆t内某金融资产的价值减少量,而α是指定的显著性水平。
2蒙特卡洛模拟的VaR计算
蒙特卡洛模拟是一种计算机模拟方法,通过模拟大量随机样本来逼近任意复杂度的系统或问题。该模拟技术被广泛运用于金融、工程和科学等多个行业。采用蒙特卡洛模拟的方法来计算VaR包括以下几个关键环节。
步骤1:确定VaR参数。
①置信水平:设定VaR计算的置信水平。置信水平通常选择95%、99%或99.9%,表示人们希望在多少概率下,资产的损失不会超过VaR值。例如,99%的置信水平意味着人们希望在99%的情况下,损失不会超过VaR值。②时间范围:确定VaR的持有期。持有期可以是一天、一周、一个月等,具体选择取决于投资者的需求和投资策略。持有期的选择将直接影响VaR的计算结果,因为时间越长,潜在的市场波动就越大。
步骤2:收集数据。
①获取原始数据:下载纳指ETF的历史价格数据。确保数据的时间跨度足够大,以便进行可靠的统计分析。②计算均值:计算该资产在过去一段时间内的平均收益率。均值是收益率的期望值,是模拟未来价格路径的重要参数。③计算标准差:计算该资产在过去一段时间内的标准差。标准差反映了收益率的波动性,是衡量风险的重要指标。计算标准差可以帮助人们了解资产的历史波动情况,从而更准确地模拟未来价格路径。
步骤3:模拟未来价格路径。
①选择模型:选用适当的随机过程模型。下文使用EViews软件进行数据分析后,最终选用几何布朗运动。几何布朗运动是一种常用的金融模型,用于模拟资产价格的随机变化。②生成随机样本:依据收益率的统计属性产生众多随机数样本。使用蒙特卡洛模拟方法,基于历史数据的均值和标准差生成大量的随机样本。这些随机样本代表可能的未来收益率。③模拟价格变化:模拟未来价格路径。对于几何布朗运动,其公式如下:
式(2)和式(3)中,St表示在时刻t的资产价值,也就是t时刻的累计净值;μ代表资产收益率的平均值;σ代表资产收益率的波动率;ε是一个随机项,假设ε遵循标准正态分布N(0,1)[3]。
步骤4:确定VaR。
①排序损失:按损失大小对所有模拟结果进行排序。②找到VaR:在已排序的损失列表中,根据预设的置信水平找到相应的VaR值。例如,若置信水平为99%,则找到最坏的1%的损失值,这个值就是VaR。③解读VaR值:VaR值提供了一个明确的指标,告诉我们在给定的置信水平和时间范围内,预计最大的损失不会超过此数值。投资者可以根据VaR值来判断其投资组合在极端市场条件下的风险。
步骤5:检验结果。
①检验模型:使用统计方法来评估违反次数是否符合预期的分布,以此检验VaR模型的性能。②调整模型:根据检验的结果,可能需要调整VaR模型的参数,如置信水平、时间范围或分布假设。如果发现实际损失超过VaR的次数过多,则可能需要提高置信水平或重新评估资产的波动性假设。通过不断调整和优化模型,确保VaR能够准确反映投资组合的风险。
3实证分析
3.1样本的选定
纳指ETF净值的波动性对其相关期权定价有显著的影响,因此选择纳指ETF的累计净值作为研究数据。具体将2022年1月4日至2024年3月6日所有交易日的累计净值(共524个数据)作为样本(数据来源于Choice金融终端)。
3.2样本的描述性统计分析
3.2.1波动的集聚性检验
股票的日收益率可以采用算术收益率或对数收益率两种不同的方法计算。相较于算数收益率,对数收益率在股票市场应用得更广泛一些,主要是因为对数收益率在处理多个连续时期的收益时更加方便,且对数收益率天然适合复利计算,可以更准确地描述股票价格随时间变化的情况,计算公式如下:
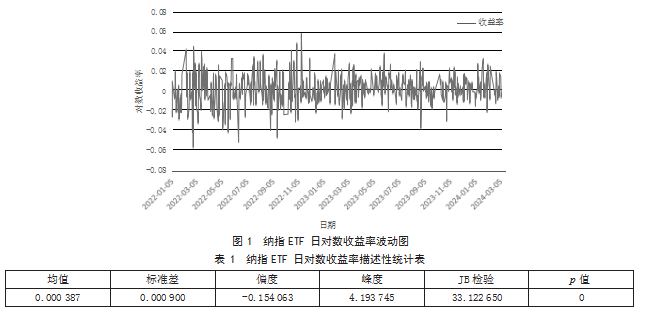
式(4)中,Pt-1、Pt分别为第t-1天和第t天的收盘价。利用EViews作出纳指ETF对数收益率图,如图1所示。
由图1可知,从2022年1月到2024年3月,纳指ETF的日对数收益率主要在零点附近上下波动,大部分日对数收益率值落在了-0.03至0.03的范围内,初步判断纳指ETF的日对数收益率具有一定程度的平稳性。然而,它们的波动性不是均匀分布的,在某些时间段内,纳指ETF的波动性相对较小;而在其他时间段,波动性显著增大,收益率变化幅度较大,这表明收益率的波动具有聚集性。
3.2.2正态性检验
为了更直观地分析收益率,接下来将使用EViews软件创建纳指ETF的日对数收益率描述性统计表,具体如表1所示。
由表1可知,纳指ETF的日对数收益率平均值为0.000 387,标准差为0.000 900,说明样本数据具有一定的离散性。收益率分布的偏度系数小于0,表明具有左偏性,这也说明了数据具有不对称性。峰度系数达到4.193 745,明显超过3,意味着相对于正态分布,收益率的分布曲线更加尖锐和陡峭。总的来说,纳指ETF的收益率展现出了“尖峰厚尾”的特性。Jarque-Bera检验的p值几乎为零,表明在99%的置信水平下可以拒绝服从正态分布的原假设[4]。
3.2.3平稳性检验
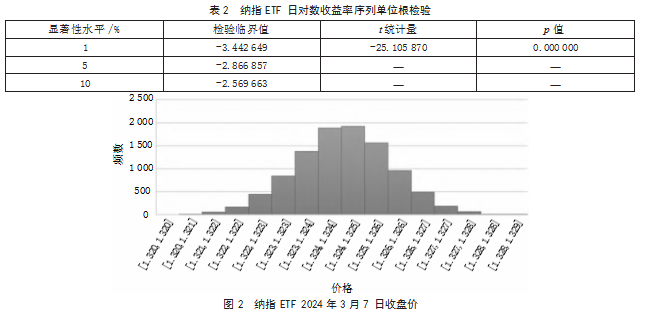
应用EViews软件执行单位根检验(即ADF Test),以评估对数收益率时间序列的平稳性,结果如表2所示。
由于ADF=-25.105 870,小于1%显著性水平的临界值-3.442 649,而且p值明显低于0.05,意味着可以拒绝原假设,即序列服从随机游走,且不含有单位根,所以可以认为日对数收益率序列是平稳序列[5]。
综合上述分析结果,可以认为纳指ETF日对数收益率服从几何布朗运动。
3.3模拟纳指ETF未来价格路径
由以上描述性统计分析结果可知:样本均值μ=0.000 387,样本标准差σ=0.000 900。取置信水平为95%,持有期为1天,并将这一天划分为50个等长的时间段,则每个时间段的平均值和标准差分别是
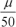
和
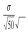
。从2024年3月6日累计净值St=1.324出发,应用几何布朗运动来模拟下一个交易日的情况,即2024年3月7日的收盘价。
采用MATLAB软件编程模拟出10 000个纳指ETF 2024年3月7日收盘价的可能价格,绘制成直方图,如图2所示。
3.4 VaR的计算
将生成的10 000个2024年3月6日的纳指ETF收盘价数据按从大到小的顺序排列,找出第9 500(10 000×95%=9 500)个数代表的收盘价。根据Excel软件运算得到S*=1.322 529 977。因此,纳指ETF从2024年3月6日到2024年3月7日持有期为1天,置信水平为95%的VaR[6]为VaR5%=St-S*=1.324-1.322 529 977=0.001 470 023,也即在95%的显著性水平上,纳指ETF在2024年3月7日这一天内可能遭受的最大损失是0.001 470 023。
3.5有效性检验
有效性检验结果能够帮助验证所使用的风险模型是否有效,即模型是否能够准确地捕捉到投资组合的风险特性。检验还可以揭示模型的不足之处,为模型的改进提供依据,从而提高模型的预测能力和稳健性,降低因模型不准确而导致的风险。
似然比检验是反映真实性的一种统计检验方法,在多个领域中广泛应用,包括但不限于分类问题、模型选择和假设检验。这里采用似然比方法进行校验,令
式(5)中,T为实际的收盘价天数,N为VaR预测失败天数,P=N/T为失败频率[7]。当T=523,置信度为95%时,可计算失败次数N的非拒绝区间为(14,33),此时观测失败次数为523×0.05=26.15,在非拒绝域内,可知纳指ETF在险价值的蒙特卡洛模拟有效。
4结束语
蒙特卡洛模拟作为一种灵活且强大的工具,为金融资产的风险度量提供了可靠的估计方法。未来将会考虑引入更多的因素来增强模型的复杂性和实用性,如考虑市场的宏观经济变量、流动性因素等对纳指ETF累计净值的潜在影响。同时,对模型的稳健性和预测能力进行进一步的检验和增强,提高投资决策精准度,降低金融市场的系统性风险。
主要参考文献
[1]谢合亮,黄卿.基于蒙特卡洛方法的金融市场风险VaR的算法分析[J].统计与决策,2017(15):157-162.
[2]李克娥,陈圣滔.基于GARCH模型的上证指数的VaR分析[J].科教文汇,2008(8):148-149.
[3]金博轶.基于Copula的投资组合均值-CVaR有效前沿分析[J].统计与决策,2010(2):34-37.
[4]伍习丽.基于高频数据的中国股市VaR风险研究[D].重庆:重庆大学,2013.
[5]梁迎双.基于波动性分析的汇率风险测度研究[D].大连:大连海事大学,2010.
[6]杨世娟,卢维学.基于蒙特卡罗模拟法的VaR计算[J].黄山学院学报,2015(3):1-4.
[7]李聪.运用GARCH族模型在不同分布下对深证综指的VaR分析[J].统计与决策,2006(17):79-80.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/80375.html
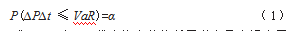
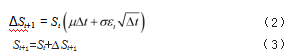

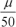 和
和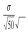 。从2024年3月6日累计净值St=1.324出发,应用几何布朗运动来模拟下一个交易日的情况,即2024年3月7日的收盘价。
。从2024年3月6日累计净值St=1.324出发,应用几何布朗运动来模拟下一个交易日的情况,即2024年3月7日的收盘价。