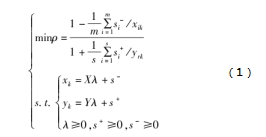【摘要】文中基于2013-2021年江苏市级面板数据,利用全局参比下超效率SBM模型、Theil指数以及Kernel核密度估计分析江苏物流业要素配置效率的地区差异及动态演进。研究表明:(1)江苏物流业要素配置效率整体处于上升阶段,其中苏南的物流业配置效率最好,苏北地区物流业配置效率最差;(2)江苏物流业配置效率的地区差异整体上呈现下降趋势,其引起地区差异的主要原因为地区内差异,其中苏北地区的地区内差异最高,苏南地区的地区内差异最低;(3)江苏物流业配置效率密度总体呈现右移趋势且右拖尾现象逐渐消失,说明江苏物流业配置效率呈现上升趋势且多极化现象减弱。
【关键词】物流业配置效率,地区差异,分布及动态演进
物流业是我国国民经济发展的动脉和重要产业,它在优化地区资源配置、改善投资营商环境、提高产业集聚效应、平衡市场供需关系和提升地区综合实力等方面有着重大作用。但目前我国物流行业的发展还存在一些问题,《“十四五”现代物流发展规划》中就指出,我国物流业存在着物流资源要素配置不合理、利用不充分、区域间发展不平衡等问题。而物流业配置效率是评价物流业发展水平的重要指标之一,通过对物流业配置效率进行测算,不仅能够充分客观地了解到地区物流业发展状况,还能为地区物流业的发展提供决策参考,因此研究物流配置效率对地区的物流发展有重要意义。
江苏作为我国经济发展最活跃、创新能力最强、开放程度最高的省份之一,属于提升创新能力和全球资源配置能力、打造引领高质量发展的第一梯队。同时,江苏物流业的发展也位于我国前列,通过测算江苏物流业配置效率并对江苏各地区物流业配置效率的地区差异及动态演进进行研究,不仅可以为优化江苏物流配置效率、减少江苏地区差异以及实现江苏高质量发展提供参考依据,同时也对其他地区物流业的发展有借鉴意义。
1文献综述
随着物流业的快速发展,物流业配置效率一直备受学术界关注,目前用于物流业配置效率测度的方法主要有两种,一种是以随机前沿函数(Stochastic Frontier Analysis,SFA)为主的参数法,于1977年由Aigner等和Meeusen,Broeck分别独立提出[1-2]。该方法假定各生产单位的生产前沿面是随机的,具有复合扰动项,将生产函数的误差项划分为随机误差和技术无效误差,技术效率根据技术无效误差来估算。相比于其他方法,SFA的优点在于它不仅可以测算每个个体的技术效率,而且可以定量分析各种相关因素对个体效率差异的具体影响,因此多被用于测算物流业配置效率。唐建荣,何硕硕采取随机前沿模型对长江经济带的物流业配置效率进行测算,发现长江经济带的下游配置效率要优于中、上游地区[3]。汪旭晖,文静怡通过随机前沿函数对我国农产品物流效率进行比较发现,目前我国中部地区的物流效率水平最高,其次是东部,西部最差[4]。另一种则是以数据包络分析(DataEnvelopmentAnalysis,DEA)为主的非参数法。该模型的基本思想是利用输入与输出之间的关系来评估决策单元(如组织或单位)的相对效率。在这个方法中,每个决策单元被视为一个点,由其输入和输出所构成的向量表示。决策单元的效率可以通过将其输入与输出的比率与其他决策单元进行比较来确定。数据包络分析法的关键是构建一个标准集合,称为“有效前沿”。有效前沿是由所有效率最高的决策单元构成的边界,其他决策单元必须在这个边界内才能被视为有效,通过度量决策单元与有效前沿的距离,可以确定它们的效率。相比于其他模型,它具有相对效率评估、无需先验权重信息、考虑多个输入输出、可拓展性和提供决策支持等优点,因此常被用于对各种资源配置效率的测算。雷勋平,刘思峰通过超效率DEA模型对2008年我国各省份的配置效率进行测算发现,当时我国还有16个省份的物流效率处于配置无效的状态[5]。江洪,李欣怡通过三阶段DEA模型测算我国各省份的物流效率,发现我国物流配置效率均处于上升趋势[6]。卢金钟等采取DEA模型从静态和动态两方面对我国西部的物流效率进行研究,结果表明目前我国西部地区在静态上呈现物流水平较低、区域差异较大的状态,在动态上呈现先降后升反复循环的状态[7]。郑梦琪则从横向角度出发分析我国黄河流域九大省份的物流效率,分析结果表明我国黄河流域的物流效率存在发展不平衡等问题[8]。
目前关于地区差异的测算主要有两种,一种是Dagum基尼系数,如程广斌等利用该方法测算中国高新技术产业创新效率的地区差异,发现我国西部地区的地区内差异要远高于其他地区[9]。另一种则是Theil指数,如孟霏等利用Theil指数测算中国战略新产业的技术创新效率时发现我国东、中、西三大地区内部差异较大[10]。
2研究方法与变量选择
2.1研究方法
2.1.1全局参比下超效率SBM模型
全局参比下超效率SBM模型(Global-Super-SBM)由杨骞等人在2021年提出,该方法结合了全局参比技术和超效率SBM技术的优点,克服了传统DEA不考虑松弛变量,不能对有效的决策单元进行比较以及决策单元不能进行跨期比较的问题[11],如式(1)所示:
其中,ρ为效率评价指标,xk和yk分别为决策单元的投入和产出向量,X和Y分别为投入和产出矩阵,i和r表示不同的评价单元,s-和s+表示投入产出的松弛变量,λ为列向量。
2.1.2Theil指数
本文选择泰尔指数(Theil)来测算江苏物流业配置效率的地区差异,该指数的优点在于能够将地区差异分解为地区间差异和地区内差异,如式(2)所示:
式中,yk为第k组市级物流配置效率均值,本文将江苏按照地理位置划分为苏南、苏北和苏中,其中苏南地区包括南京、苏州、无锡、镇江和常州,苏北地区包括盐城、徐州、宿迁、淮安和连云港,苏中地区包括泰州、徐州和南通;nk为第k组市级数量数目。
2.1.3Kernel核密度估计
通过Theil指数能够分析江苏物流业配置效率的地区差异及其来源,但未能反映绝对差异的动态分布及其演进规律,因此,本文利用Kernel核密度方法进一步分析江苏三大地区物流区域配置效率的分布态势、分布延展性以及极化趋势。假设x1,…,xn为独立同分布的样本,其概率密度函数为f(x),则在点x处的概率密度表达式如式(6)所示:
2.2变量选取
本文参考范振伟,刘华琼和曹炳汝,邓莉娟的研究[12-13],结合数据的可获得性,确定物流业投入产出指标如表1所示,其中,交通运输、仓储和邮政业城镇单位就业人数用来衡量人力资源投入,交通运输、仓储和邮政业全社会固定投资用来衡量财力资源投入,等级公路里程用来衡量物力资源投入。以下数据来源于《江苏统计年鉴》和江苏地方统计年鉴,部分缺失数据采取线性回归法进行补齐。
3实证分析
3.1江苏物流业配置效率测度
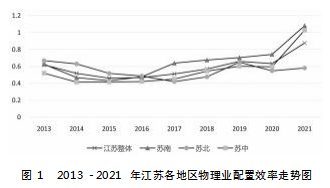
本文采取全局参比下超效率SBM模型对江苏物流配置效率进行测算,结果如图1所示。从整体上来看,江苏物流业配置效率值由0.6187上升至0.8768,上升幅度达41.71%,表明2013-2021年江苏物流业配置效率呈现明显的上升的趋势。从三大地区来看,苏南和苏中配置效率呈现不断的上升趋势,苏北则呈现先下降后上升的趋势,同时苏南的配置效率常年位于三大地区的首位,其次为苏中,苏北配置效率最差,这可能与当地的经济发展情况有关。
3.2空间差异分析
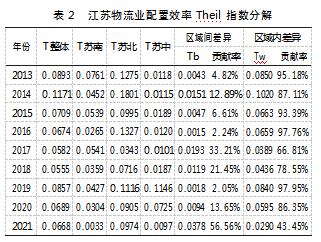
本文采取Theil指数分析江苏物流配置效率地区差异的原因,其结果如表2所示。从整体上来看,指数值由2013年的0.0893下降至2021年的0.0668,降幅达到25.19%,表明在2013-2021年间江苏物流业配置效率正朝均衡方向发展,这意味着江苏在统筹构建优势互补的区域协调布局方面成效显著。从三大地区来看,苏南、苏北和苏中的Theil指数均呈现不同程度的下降,其中下降幅度最大的是苏南地区,下降幅度最小的是苏北地区,说明苏南地区在减少地区差异上成效明显,同时从数值上可以看出,目前区域差异最大的地区是苏北地区,其次是苏中,最后为苏南地区。从区域间和区域内差异来看,区域间差异波动上升,区域内差异波动下降,表明三大地区间差异愈发扩大,区域内差异愈发缩小。从贡献率来看,区域内差异是是引起江苏物流业配置效率差异的主要原因。
3.3江苏物流业配置效率的Kernel核密度
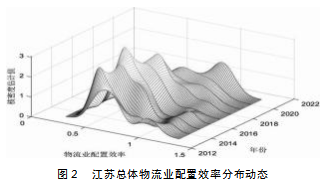
为了探究江苏省物流业配置效率的地区差异,本文采取Kernel核密度估计对江苏省的物流业配置效率进行分析,分析结果如图2所示。从图2中可以看出,江苏在物流业配置效率的动态分布上呈现如下几点特征:第一,从分布位置上来看,Kernel核密度函数的中心呈现右移趋势,这意味着江苏物流配置效率在不断上升;第二,从分布形态来看,主峰峰值呈现先上升再下降的趋势,这表明江苏各地区之间物流业配置效率的差距呈现先上升后下降的态势;第三,从延展性分析,江苏物流业配置效率的核密度函数的右拖尾现象呈现减弱趋势,这表明江苏物流业配置效率极化现象在减弱。
4结论
本文首先采取全局参比下超效率SBM模型测算2013-2021年江苏各地区物流业配置效率,其次运用Theil指数分解江苏物流业配置效率的空间差异特征,最后运用Kernel核密度估计法分析其演变趋势,得出如下结论:
①通过考察2013-2021年江苏物流业配置效率,发现江苏物流业配置效率在整体上呈现上升趋势。从地区层面上来看,三大地区也均呈现明显的上升趋势,其中苏南地区的物流业配置效率最高,苏中次之,苏北物流业配置效率最低。
②江苏物流业配置效率的总体空间差异整体呈现下降趋势,地区内差异是江苏物流业配置效率区域总体差异的主要原因。从地区角度来看,江苏三大地区的物流业配置效率的区域内差异整体上都呈现下降趋势,其中区域内差异最小的为苏南,最大的为苏北。
③首先,从分布位置来看,Kernel核密度函数的中心呈现右移趋势,这意味着江苏物流业配置效率在不断上升。其次,从分布形态来看,主峰峰值呈现先上升再下降的趋势,这表明江苏各地区之间物流业配置效率的差距呈现先上升后下降的态势。最后,从延展性来看,江苏物流业配置效率的核密度函数的右拖尾现象呈现减弱趋势,这表明江苏物流业配置效率极化现象在减弱。
[参考文献]
[1]Aigner,D.J.,Lovell,C.A.K.,Schmidt,P.Formulation and Estimation of Stochastic Frontier Production Function Models[J].Journal of Econometrics,1977,6(1):21-37.
[2]Meeusen W.,Broeck,J.V..Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error[J].
[3]唐建荣,何硕硕.长江经济带物流业要素配置效率变化研究[J].物流科技,2023,46(05):1-7.
[4]汪旭晖,文静怡.我国农产品物流效率及其区域差异—基于省际面板数据的SFA分析[J].当代经济管理,2015,37(01):26-32.
[5]雷勋平,刘思峰.基于DEA的物流产业效率测度实证研究—基于我国31个省、市、自治区2008年投入产出数据[J].华东经济管理,2012,26(07):62-66.
[6]江洪,李欣怡.中国省际物流业效率研究—基于三阶段DEA模型[J].辽宁工程技术大学学报(社会科学版),2023,25(05):335-341+364.
[7]卢金钟,贺玉峥,李煖,等.西部地区物流效率评价研究[J].物流工程与管理,2024,46(01):149-153.
[8]郑梦琪.基于DEA模型的黄河流域物流效率分析[J].物流工程与管理,2022,44(06):34-36+21.
[9]程广斌,赵川,李祎.中国高技术产业创新效率的地区差异及动态演进[J].统计与决策,2023,39(02):173-178.
[10]孟霏,鲁志国,高粼彤.中国战略性新兴产业技术创新效率时空演化及驱动因素分析[J].统计与决策,2023,39(16):91-95.
[11]杨骞,刘鑫鹏,孙淑惠.中国科技创新效率的时空格局及收敛性检验[J].数量经济技术经济研究,2021,38(12):105-123.
[12]范振伟,刘华琼.测算和分析杭州湾核心城市群物流效率及其影响因素[J].物流工程与管理,2024,46(03):94-97.
[13]曹炳汝,邓莉娟.长江经济带物流业效率增长影响因素[J].经济地理,2019,39(07):148-157.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/79459.html