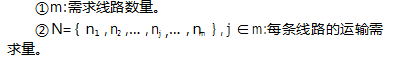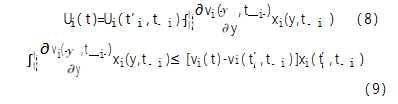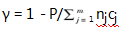【摘要】在物流运输服务交易市场,二级市场不断增长,导致供应商面临关联价值的信息结构。关联价值模型允许竞拍者根据其他竞拍者的信息估价,挑战传统私人价值信息结构下的交易机制。文中设计了关联价值情境下的最优运输服务组合拍卖机制,以促使真实信息提交。该机制满足激励相容性与个体理性,允许投标人充分表达其偏好,降低托运人采购成本。理论分析表明该机制有效,实验证实能降低采购成本。
【关键词】物流运输采购,关联价值,组合拍卖,拍卖机制
电子商务交易额在2021年达到37.2万亿元,2022年上升至43.83万亿元,电商物流占据我国物流业最大份额。运输服务交易(LSTs)成为电商物流关注的焦点,供应链管理直接影响企业稳定、持续的发展[1],以及物流市场效率和交易量[2-3]。但随着电商物流的快速发展,LST市场信息不对称问题加剧,垄断、合谋行为增多,导致市场公平性下降,效率降低,迫切需要激励运输商真实报价的机制设计。
运输服务交易方式包括目录、拍卖、谈判。拍卖因其竞争性、高效、节省时间等特点备受关注[2,4-5]。运输服务交易市场存在广泛的二级市场,运输商考虑将已签订的运输服务合同转售给其他运输商[6],且市场偏好存在多样性与动态性[7],这使得运输商处于关联价值信息结构,显著影响了物流运输服务市场的交易效率,并增加了机制诱导竞标人“说真话”的难度。目前的运输服务拍卖机制主要适用于私人价值的信息结构,尽管已有部分学者在关联价值下进行了拍卖机制的研究,但针对物流市场尚未有相关成果[7-12]。因此,在运输服务交易机制的设计中考虑关联价值的影响很有必要。
本文以我国物流运输服务采购问题为背景,提出了关联价值信息结构下的最优采购机制。以组合拍卖的形式,允许承运人充分表达其投标偏好,减少承运人空载里程,避免出现问题[13-22],通过数学建模解决了如何体现关联价值、机制目标是什么、如何满足激励相容性等问题。理论证明该机制可实现激励相容性、满足个体理性,并最终验证了该机制在降低采购成本方面的有效性。
1假设与符号设置
托运人需要公布三个信息:①运输目的地的数量(需求线路);②每个目的地的运输需求量;③每条线路的保留价格,即托运人购买运输服务的最高可承担价格。
承运人需要提交三个信息:①服务方案(投标线路);②每个服务方案的成本函数;③成本信号。
在后面的内容中,每个始发地与目的地的运输路线全部用“线路”表示[23-24]。
相关假设和符号说明如下:
2关联价值下最优运输服务采购组合拍卖机制
2.1模型设计
根据著名的显示原理[25],托运人可以将最优拍卖机制简化为一个直接机制,即在此机制下,承运人真实地提交其类型,托运人再根据承运人提交的类型决定最优的分配结果X:t→{0,1}mn2|G|和支付P:t→Rn。其中,分配方式xi(·)=1表示承运商i成功中标,否则为0。
当承运人真实提交自己的类型ω时,托运人的期望支付为:
其中:约束(4)为事后激励相容约束,表示参与人真实提交自己的类型会获得最大的效用;约束(5)为事后个体理性约束,表示承运商只要参与拍卖就会获得非负的效用;约束(6)为数量约束,表示同一目的地中被分配出去的订单量不会超过托运人的需求量;约束(7)为决策条件,当承运人i中标时为1,否则为0。
因此,最优机制设计问题可以表述为:在满足约束(4)-(7)下寻找能够最小化式(3)的可行机制(x,p)。
2.2模型求解
根据Myerson对离线拍卖机制的研究方法,直接机制(x,p)满足激励相容约束(4)和个体理性约束(5),当且仅当下列条件成立:
由此,式(12)使得机制(x,p)满足约束条件(9)和(10),在满足条件(6)(7)和(8)下,最小化式(12)的分配规则xi(t)∈(0,1),∀i与支付规则(11)组成了最优机制(x,p)。
3采购流程
综合上文设计的最优机制,给出该机制采购的具体实施程序:
①托运人发布自己采购的基本需求,并宣布一定的投标规则,包括投标开始与结束时间,线路组合数量,每个承运人根据投标规则提交自己的类型ωi和估值函数vi(t)以及自己的信号ti。
②托运人将所有承运人信息汇总为类型集合ω、估值函数集合v、信号集合t以及参与人集合I,与自己的信息汇总为目的地需求集合M,数量需求集合N和自运成本集合C,并输入至Matlab软件中。
③计算机通过软件在约束条件(4)-(7)下求解目标函数(11),得到分配结果xi(t)∈χ,当xi(t)=1时,表明承运人中标,反之未中标。
④对于任意中标的承运人i,通过式(12)计算出需要对托运人支付的金额pi(t)。
⑤根据机制确定的分配结果与支付金额,与相应中标的承运商签订运输合同,并支付一定定金,承运商完成所有指定的运输任务后,托运人支付剩余金额,完成采购。
4数值实验
在本节中,我们将应用Matlab软件进行数值实验,以对两种机制的性能能进行验证。具体而言,我们将设置15个承运人参与竞标,通过软件自动生成承运人的成本信号、投标内容、成本函数集合,然后根据最后的分配结果探讨机制的性能表现。性能指标:成本节省率
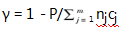
4.1实验设置
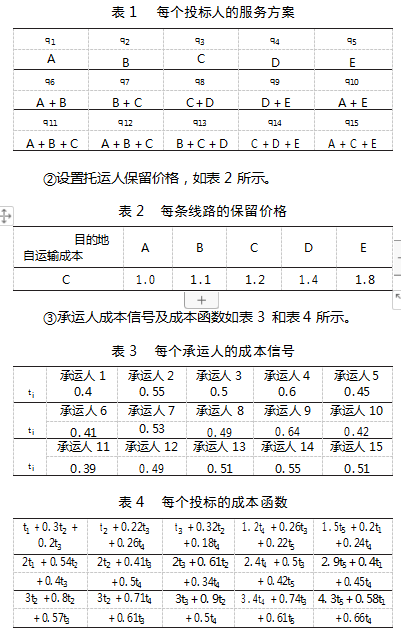
根据阿里巴巴在2021年10月公布的交易信息,不同承运商的交易价格在[0.87,1.64]千美元/吨。由于承运商的运输成本为商业隐私,因此我们只能通过交易价格假设承运商的运输成本在[0.62,1.6]千美元/吨之间,托运人的自运输成本范围为[0.85,1.85]千美元/吨。由此,我们生成如下参数。
①实验设置A,B,C,D,E五个运输目的地,每个目的地的运输需求量分别为3单位,4单位,3单位,3单位,2单位。承运人数为15,每个承运商自动生成一种服务方案,记为q i。具体投标内容如下表1所示。
4.2结果分析
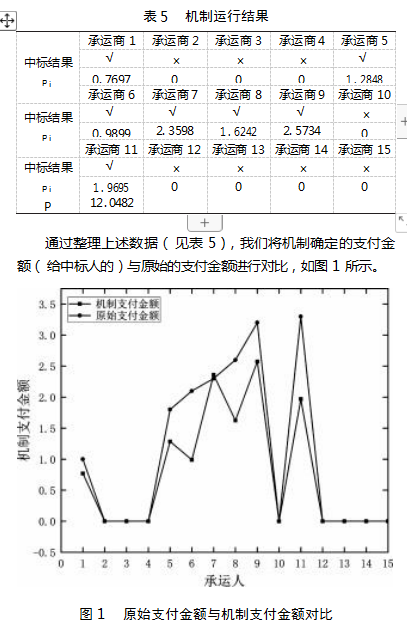
在表5中我们列举了机制运行的分配结果与相应的支付金额,从图1中可以发现,对于中标的托运人,通过该机制确定的支付金额均小于原始的运输费用。经计算可得,使用机制前,托运人的采购成本是18.8,使用机制后的采购成本是12.0482,节省率达35.91%。
综上所述,该机制以最小化托运人采购成本为目标,有效减少了托运人的采购成本,并且通过激励相容性与个体理性约束,保证了机制的高效性与公平性。
5结束语
为帮助托运人在关联价值环境下以最低的金额支付采购运输服务费用,本文使用机制设计的方法将物流运输服务采购问题建模为组合拍卖,提出了关联价值最优物流运输服务采购机制。拍卖的采购方式具有高度自动化,可以在信息不对称和供需动态变化的环境中实现高效率分配,减少空间限制导致的交易成本。本文提出的机制考虑了运输商在不同线路上的互补性与替代性,使他们能充分表达自己的偏好,并被证明满足IC和IR的要求,能激励投标人真实地提交自己的信息,从而提高交易的公平性并降低投标人的决策负担。
我们的工作首次为关联价值环境中的运输服务交易市场设计了拍卖机制,为以后的研究奠定了基础。但在关联价值下的拍卖机制研究工作依然存在很多难题,且到目前为止的研究成果还非常有限,本文在一些更细节和更深刻的方向仍有很大的探索空间,如改进机制适用情况的细化,更普适的正则性条件设计,更复杂的关联函数研究等,这也将成为未来研究的主要方向。
[参考文献]
[1]Myerson R B.Optimal auction design[J].Mathematics of Operations Research,1981,6(1):58-73.
[2]Lafkihi M,Pan S,Ballot E.Freight transportation service procurement:A literature review and future research opportunities in omnichannel e-commerce[J].Transportation Research Part E:Logistics and Transportation Review,2019,125:348-365.
[3]Yu H,Huang M,Chao X,et al.Truthful multi-attributemulti-unit double auctions for B2B e-commerce logistics service transactions[J].Transportation Research Part E: Logistics and Transportation Review,2022,164:102814.
[4]Caplice,C.Electronic markets for truckload transportation[J].Prod.Oper.Manag.,2009,16(4):423-436.
[5]Bellantuono,N.,Ettorre,D.,Kersten,G.E.,Pontrandolfo,P.Multi-attribute auction and negotiation for e-procurement of logistics[J].Group Decis.Negot.,2014,23(3):421-441.
[6]Xu S X,Huang G Q,Cheng M.Truthful,budget-balanced bundle double auctions for carrier collaboration[J].Transportation Science,2017,51(4):1365-1386.
[7]褚煜琪,孔兰兰.消费者偏好视角下的供应链研究现状及趋势—基于CiteSpace的知识图谱分析[J].物流工程与管理,2024,46(01):64-70.
[8]Constantin F,Ito T,Parkes D C.Online Auctions for Bidders with Interdependent Values[C]Proceedings of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems,2007:1-3.
[9]ÜlküL.Optimal combinatorial mechanism design[J].Economic Theory,2013,53:473-498.
[10]Wang,Y.Wang,X.Application of multi-unit combinatorial auction in the initial allocation of pollution rights[J].China Rural Water Conservancy and Hydropower,2015(9):194-197.
[11]Eden A,Feldman M,Fiat A,et al.Combinatorial Auctions with Interdependent Valuations:SOS to the Rescue[C].Proceedings of the 2019 ACM Conference on Economics and Computation,2019:19-20.
[12]Li,Y.Approximation in Mechanism Design with Interdependent Values[C].In ACM Conference on Electronic Commerce,2013:675-676.
[13]Rao C,Zhao Y,Ma S.Procurement decision making mechanism of divisible goods based on multi-attribute auction[J].Electronic Commerce Research and Applications,2012,11(4):397-406.
[14]Chu,L.Y.Truthful bundle/multiunit double auctions[J].Manage.Sci.,2009,55(7):1184-1198.
[15]De Vries,S.,Vohra,R.V.Combinatorial auctions:A survey [J].INFORMS J.Comput.,2003,15(3):284-309.
[16]Song J,Regan A.Combinatorial auctions for transportation service procurement:The carrier perspective[J].Transportation Research Record,2003,1833(1):40-46.
[17]Caplice C,Sheffi Y.Combinatorial auctions for truckload transportation[J].Combinatorial Auctions,2006,21:539-571.
[18]Sheffi,Y.Combinatorial auctions in the procurement of transportation services[J].INFORMS Journal on Applied Analytics,2004,34(4):245-252.
[19]Chang,T.S.Decision support for truckload carriers in one-shot combinatorial auctions[J].Transportation Research Part B:Methodological,2009,43(5):522-541.
[20]Robu,V.,Noot,H.,Poutré,H.L.,van Schijndel,W.-J.Amulti-agent platform for auction-based allocation of loadsin transportation logistics[J].Expert Systems with Applications,2011,38(4):3483-3491.
[21]Li G,Li L,Sun J.Pricing and service effort strategy in a dual-channel supply chain with showrooming effect[J].Transportation Research Part E:Logistics and Transportation Review,2019,126:32-48.
[22]Lyu K,Chen H,Che A.A bid generation problem in truckload transportation service procurement considering multiple periods and uncertainty:Model and benders decomposition approach[J].IEEE Transactions on Intelligent Transportation Systems,2021,23(7):9157-9170.
[23]Robu V,Parkes D C,Ito T,et al.Efficient Interdependent Value Combinatorial Auctions with Single Minded Bidders[C].Proceedings of the 23rd International Joint Corference on Artificial Intelligence,2013:339-345.
[24]Song,J.,Regan,A.Approximation algorithms for the bid construction problem in combinatorial auctions for the procurement of freight transportation contracts[J].Transportation Research Part B:Methodological,2005,39(10):914-933.
[25]Lee,C.-G.,Kwon,R.H.,Ma,Z.A carrier's optimal bidgeneration problem in combinatorial auctions for transportation procurement[J].Transportation Research Part E:Logistics and Transportation Review,2007,43(2):173-191.
[26]乔湫娟.供应链管理模式下企业物流管理完善建议[J].物流工程与管理,2023,45(03):64-66.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/78326.html