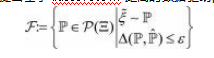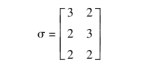【摘要】随着可持续发展理念得到社会广泛认同,企业开始逐步关注供应链运作中资源的回收利用。为了合理规划资源,构建了以供应链总成本为目标,考虑多主体参与的闭环供应链混合整数规划模型。进一步考虑了采购价格不确定,结合分布式鲁棒优化方法,使用数据驱动模糊集模拟不确定参数的真实分布,并融入均值-CVaR方法衡量决策者的风险规避特征,通过对偶理论将模型转化为可处理的线性问题。随后在Python中调用Gurobi求解器对模型求解,结果显示分布式鲁棒优化可以较好地处理决策过程中不确定参数的影响,并且模型可以为不同决策偏好以及不同目标预算下的决策提供支持,最后通过灵敏度分析再次验证了模型的实用性。
【关键词】采购价格不确定,分布式鲁棒优化,均值-CVaR
随着可持续发展理念得到社会广泛认同,经济的快速发展以及市场竞争的不断加剧等因素使闭环供应链和集成物流成为企业和政府关注的重点[1]。为了减轻对环境的影响,多国政府也相继出台法规,通过强制性手段要求企业对各种产品进行回收再利用[2]。因此,企业所关注的不再只是零部件的获取与加工、制造、分销、产品的使用与维护等,还需要将产品的回收、拆卸、再利用以及报废处理等一系列活动加入到传统供应链网络当中,形成新的闭环供应链网络结构。
在供应链中,生产的数量以及与零部件相关的决策都受到采购成本的影响,并且通常情况下,这些不确定因素不在企业的可控制范围之内。虽然企业可以通过市场营销和产品定价来影响这些参数,但由于外部环境的变化,无法真实预测这些参数的准确值。此外,在闭环供应链中,零部件的来源有两种,导致与零部件相关的决策变得更加复杂,这种不确定性使得企业在决策过程中面临一些风险,需要妥善处理。目前不确定参数的处理方式主要有随机优化与鲁棒优化[3],随机优化假设不确定变量服从于某一特定分布,求得期望最优的结果,Namdar等[4]假设中断发生后市场信息服从均匀分布,以此研究多场景下的最优采购策略。Merzifonluoglu[5]假设客户需求与现货价格随机变量服从正态分布情况下的最优决策。Maryam,Ramin[6]考虑了绿色供应链设计中的需求、供应、加工、运输、短缺以及容量扩展成本的不确定性,构建了一个不确定性环境下的多目标随机规划模型。随机规划虽然可以处理不确定参数问题,但需要通过参数的概率分布计算出期望的方式确定随机参数,这就导致随机规划在处理问题时,需要得知参数真实的概率分布,所以随机规划概率分布与实际往往存在误差,会影响决策的有效性。鲁棒优化在一定程度上弥补了随机规划的缺点,可通过构建随机参数的不确定集来求解最差情况下的最优解。张英,魏明珠[7]利用鲁棒优化解决了逆向物流中回收环境的不确定性。Zetina等[8]通过构建预算不确定集考虑需求与运输成本的不确定性的经典鲁棒优化研究了hub选址问题。Mirzaee等[9]考虑了绿色供应商选择问题中的需求、成本以及退货比例等的不确定性,构建了一种多目标鲁棒优化模型。Alavi,Jabbarzadeh[10]提出了一个随机鲁棒优化模型,在需求不确定的情况下帮助决策者确定设施数量和位置以及融资决策。虽然鲁棒相比于随机规划可以更好地处理参数不确定问题,但是根据鲁棒优化的定义不难发现,鲁棒优化也存在过于保守的缺点。
分布式鲁棒优化结合了随机规划与鲁棒优化的特点,旨在寻求最差分布下的最优决策,这一思路弥补了随机规划与鲁棒优化的缺点,更符合现代化供应链的决策思路。Cecil等[11]提出了一个考虑供给、价格、需求不确定的多时期多目标分布式鲁棒优化模型,用来提升个人防护装备的抗疫情干扰能力。张玲等[12-13]通过分布式鲁棒优化解决灾后临时献血点选址问题以及应急血液供应网络设计问题中的需求不确定性。Zhang等[14]提出了考虑需求、运输时间、安全因素不确定情况下的分布鲁棒优化模型,用来提高灾后医疗救援供应链运作效率。Wang等[15]考虑了设施选址问题中的需求以及运输成本的不确定性,并且在数值实验中比较了DRO和SO,RO模型解的优劣性。但是不论是随机规划、鲁棒优化还是分布式鲁棒优化,都没有考虑决策者的风险规避特征,而在解决实际问题时,决策者对待风险的态度对决策结果有着较大的影响,需要在决策过程中衡量决策者的风险规避特征。
目前,广泛用来衡量风险规避特征的方法是条件风险值(CVaR),Cavus等[16]利用条件风险值衡量因不确定性流量产生的随机总成本。Dixit等[17]使用条件风险值在供应链高负载的条件下观察影响和低概率风险。Tao等[18]提出了一种衡量不及时交货惩罚的CVaR衡量标准,用来衡量决策者的风险规避态度对决策结果的影响。均值-CVaR可以统筹风险成本与期望成本,既解决了风险测度问题,同时也克服了期望值模型的低效性,在不确定性研究中引入CVaR方法更应该被重视。
综上所述,本文将分布式鲁棒优化结合均值-CVaR来解决采购价格不确定下的闭环供应设计问题。分布式鲁棒优化的最终形式取决于模糊集,但是模糊集形式众多,在当前的大数据背景下,数据的获取相对容易,通过历史数据形成的经验分布近似模拟的真实分布比均值、协方差等统计数据更能描绘出参数的真实分布。并且为了减少过拟合,本文采用了考虑目标预算形式的分布式鲁棒优化。
1问题描述及模型构建
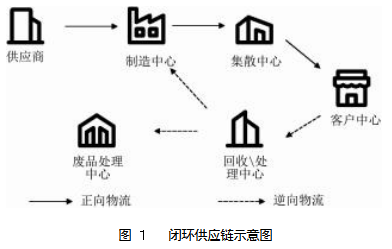
本文研究了单周期、多种零部件、多产品的闭环供应链网络,包括供应商、生产中心、配送中心、客户中心、回收中心以及处理中心(见图1)。在整个供应链中,供应商为供给点、客户中心为需求点,其数量和位置是预先确定的,制造中心向供应商采购多种零部件生产成多种商品后,经由分销商运往客户中心,其中每个节点都可以和多个上级节点形成供应关系。部分成品由回收中心回收,并在回收中心内完成拆解,可再次利用的零部件被送到制造中心,拆卸的其余废品送往处理中心进行集中处理。模型所需要做出的决策包括各节点的选址问题,各节点间的运输关系以及各节点间的流量。
1.2基本假设
①每种产品的生产都需要多种材料;
②除所需采购的关键零部件,其余材料数量充足;
③节点之间存在最大流量约束;
④不考虑节点库存冗余。
1.3模型构建
考虑供应链运营总成本的目标函数如下:
第一部分为开放固定设施的固定成本
目标函数(4)表示最小化供应链运营成本;约束(5)表示制造中心零部件与生产成品平衡;约束(6)表示制造中心与集散中心流量平衡约束;约束(7)表示满足客户需求;约束(8)表示回收数量与回收中心处理数量平衡;约束(9)(10)分别表示可再利用零部件与不可再利用零部件与回收数量的平衡;约束(11)表示缺货数量上限约束;约束(12)-(16)表示节点能力上限约束;约束(17)(18)表示各变量取值范围。
2模型转化
在实际问题中,在进行事前决策时通常无法获得模型中某一参数的真实分布,但是可以通过历史数据近似模拟不确定参数的分布。为了处理本文所提出模型中的参数不确定性问题,本文提出基于Wasserstein距离的数据驱动模糊集:
在风险中性的条件下,预期成本方法可帮助企业提高供应链整体运作效率。但是从长期来看,风险中性的最小化成本并不一直是最优的,因为当供应价格存在不确定性时,风险是存在的,连续的巨大损失会威胁到企业的正常运作,所以需要对决策的风险偏好性进行衡量。
风险价值法(VaR)是金融学中用来度量金融风险的一种常用方法。它是一种有效且简单的风险管理工具,但是存在一定的缺陷:VaR不具备一致性,组合总风险值可能大于组合内部各风险值之和;VaR没有考虑尾部损失,即超过最大损失值的那一部分,并且VaR的计算结果对于这一部分往往持有乐观态度,但事实并非如此,过于严重的中断损失可能会导致企业的破产,这与以保守为主导的商业决策相违背。CVaR弥补了VaR无法衡量超过最大损失部分的风险,其代表了超额损失的条件均值。虽然CVaR预测了超额损失部分,但却忽略了原有的成本部分,使得整体决策目标偏低,所以本文采用均值-CVaR来衡量决策偏好对风险成本的影响,所需要求解的形式如下:
3数值实验
3.1算例背景
本部分将用一个数值算例来说明所设计韧性供应链决策准则的有效性,由于无法获得全部的真实数据,其中部分数据会进行一定程度的合理假设。在实际的供应链运作中,所需的数据可以从多个来源获取。算例背景为长三角地区ofo共享单车,本文考虑生产共享单车所需的25种零件中的3种主要零件(M1-M3),生产ofo(P1)和ofocurve(P2)两种主要车型。现设置10个潜在供应商(I1-I10);4个潜在制造中心(J1-J4);4个潜在集散中心(N1-N4);5个固定客户区(H1-H5);3个潜在回收中心(K1-K3);2个潜在废品处理中心(V1-V2)。本文运输成本参考国内主要物流承运商的平均费率,零部件(M1-M3)与(P1,P2)之间的转化系数σ如下
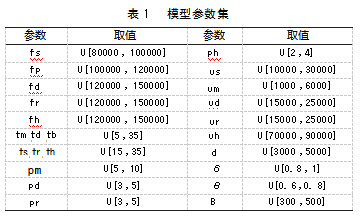
本文基于供应价格和需求不确定所建立的模糊集是通过历史数据的经验分布来近似模拟真实分布的,并且经验分布是建立在N条历史数据点上的离散均匀分布,即每个历史样本均会成为不确定参数的支撑点,历史样本数量越多以及样本越具一般性对不确定参数的真实分布描绘越精确,但同时也会增大问题规模和增加计算时间,故样本数量需要针对具体的参数类型变化。本文所采用的历史数据样本数量为20组,价格数据区间为[15,45],三种零部件上限ξ为[45,30,30]。表1展示了模型中一些其他相关参数的取值,这些参数取值均服从一定范围内的均匀分布。
根据上述模型,计算得到Z0值为14202948。本文将分别考虑ρ为2%、4%、6%、8%、10%和12%六种预算成本下的最优决策。
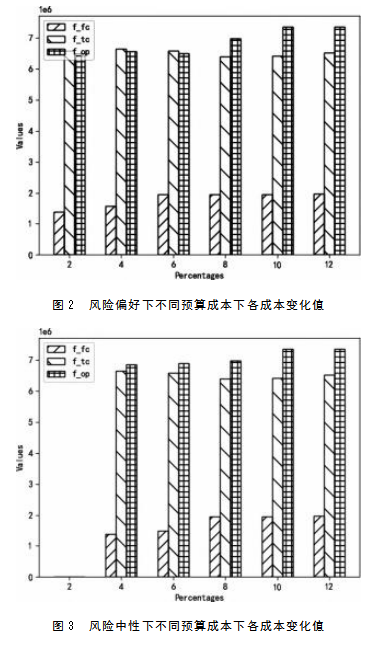
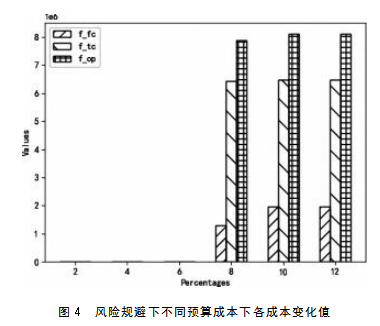
由于本文考虑了条件风险值CVaR,所以需要考虑不同风险偏好下的最优决策,文中考虑了三种不同的风险偏好,分别是风险偏好(λ=0.1,β=0.5),风险中性(λ=0.5,β=0.7),风险规避(λ=0.9,β=0.9)。图2展示了风险偏好下不同预算成本下各成本的变化值,图3展示了风险中性下不同预算成本下的各成本变化值,图4展示了风险规避下不同预算成本下的各成本变化值。从图中可知,虽然不确定性发生在运营成本中,但是随着预算成本的提高,各项成本均有不同程度的提高并逐步趋于平稳。在风险偏好下,预算成本的提高会影响选址固定成本,在该决策下,更偏向于选择多供应商承担零部件供应。在风险中性与风险规避下,ρ低于2%时风险中性模型无解,低于8%时风险规避模型无解,表明过低的预算不能够平衡不确定性带来的决策风险,并且随着预算成本的提高,决策结果同样偏向构建更多主体参与的供应网络。
除了目标成本,决策结果之间也存在较大差异。在风险偏好下,ρ为2%时,选址结果为供应商X1、X4、X7、X8、X9,制造中心Y2、Y4,分销中心N2、N4,回收中心G2以及废品处理中心V1,其中每个供应商均服务于制造中心Y2与Y4。这说明在预算充足的情况下,多源采购是主要决策方式,并且分销中心向制造中心采购时,均有主要采购目标以及辅助采购目标;随着预算成本的增加,节点数量的选择结果逐步增加,并且各节点间流量关系也随之变化,更趋向于快速、高效的供应网络。由此可见,提高一定的总预算成本,不仅能抵御不确定性带来的风险,也可以有效提升供应网络的运作效率。
3.3对比分析
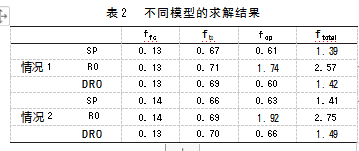
为了验证分布式鲁棒优化(DRO)在处理不确定参数问题时优于随机规划(SP)与传统鲁棒优化(RO),本文对这三种模型的求解结果进行对比分析,其中鲁棒优化采用盒式不确定集形式。为了有效地进行对比,本文设置了另一组数据集,该集相比于原求解集合,离散程度更大,用来模拟不确定性更强的情况,求解结果如表2所示(1e7)。
根据表2可知,由于过度的保守性,RO模型只求解最坏情况下的最优决策,在本文中则取各历史数据中的最大值,所以导致两种情况下成本远高于SP模型与DRO模型,并且主要体现在运营成本中;同时,供应链需求满足率也只有80%,这是由于随着运营成本的增加,单位缺货成本超过了单位成本,从求解结果来看,RO模型并不适合用来辅助现实生活中的供应链决策;SP模型在两种情况下的求解结果并无明显差异,这是因为本文两个数据集在离散程度上有较大差异,但是均值上的变化并不明显,SP模型只考虑均值,所以导致最终求解结果无明显变化,这也说明SP模型完全忽略了数据的随机性,同样不适合辅助现实生活中的供应链决策。DRO模型在两种情况下的求解结果不论是在目标成本还是决策结果都有一定的差异性,虽然相比SP模型,总成本存在少量提升,但是DRO模型充分考虑了数据的趋势与随机性。例如,根据本文的数据设置供应商I4和I7的离散程度相近且均值相同,但是I4的价格普遍偏高,只有过少量的大幅降低,而I7的价格普遍处在平均水平以下,只有少量的增加,这些变动都是来自于市场的波动,不可以忽略,而SP模型则忽略趋势带来的影响,只从均值方面考虑从而同等看待两个供应商,而DRO模型则会充分考虑趋势所带来的影响。
3.4灵敏度分析
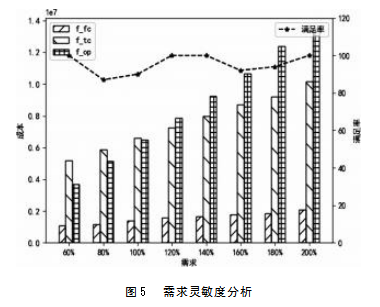
为了验证模型在不同情形下所做出决策的实用性,本文针对文中几个重要参数做了灵敏度分析,而为了呈现结果的特点,该部分将预算值固定,考虑不同决策偏好下的各成本以及决策结果变化。首先考虑需求的灵敏度分析,在其他参数不变的情况下,将需求改变至原基础的60%、80%、100%、120%、140%、160%、180%以及200%,结果如图5所示
随着需求的逐渐增加,各项成本也逐渐增加,其中当成本变动比例处在120%以下时,运输成本占据主要部分,从120%开始,运营成本增加较为明显,逐渐占据总成本的主要部分,节点固定成本在缓慢增长过后逐渐趋于平稳。当变动比例为80%、100%、160%、180%时,需求满足率出现了未满足的情况,这是由于需求增加到略高于节点能力的水平时,额外增加节点的成本会远大于缺货所产生的额外成本,当后续需求再次增加时,增加节点数量相比于大量缺货会更加合理。
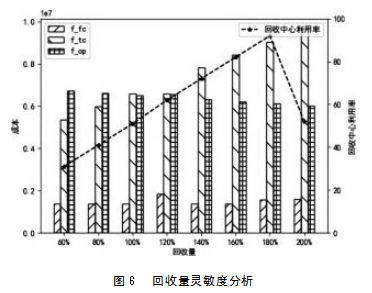
本文将回收数量也设置为原基础的60%、80%、100%、120%、140%、160%、180%以及200%,以了解各成本的变动情况以及决策结果的不同,结果如图6所示。
随着回收量的增加,各成本也在发生明显的波动,当回收量变动比例小于100%时,主要成本为运营成本,当回收量增加时,运营成本保持平稳并缓慢下降,运输成本快速增长并占据总成本中的主导地位,这是由于回收与拆卸成本比制造成本低,所以回收数量的增加一定程度上降低了零部件的采购成本,但是回收数量以及可用零部件再利用和废料的处理增加了大量的运输成本;此外,在回收量增加的过程中回收中心的利用率也在逐步增加,但是当回收量超过上限时,不仅使额外的节点成本增加了,同时也使回收率处在一个较低的水平。
4结论
本文构建了一个多零部件、多产品、多主体参与的闭环供应链网络,建立了以供应链总成本为目标的混合整数规划模型。本文考虑了零部件供应价格不确定,构建了基于数据驱动模糊集的分布式鲁棒优化模型,同时引入了均值-CVaR度量决策者的风险规避特征。为了便于计算,增加模型的实用性,本文基于对偶理论将分布式鲁棒优化部分转化为可处理的线性问题,通过计算结果以及灵敏度分析结果验证了模型在处理参数不确定问题时的有效性以及能为不同决策偏好提供决策支持。根据上述的数值实验与灵敏度分析,本文得出结论:(1)充分利用历史数据辅助决策过程,分布式鲁棒优化模型可以不局限于数据的种类与形式,越精细的数据越有利于提升决策的有效性。(2)充分考虑决策偏好,不确定性环境下,适当提高目标成本可以有效地规避不确定性所带来的决策风险。
在未来的研究中将考虑更多参数如需求、回收率等的不确定性,进一步考虑节点间不同运输方式、回收方式等多形式的闭环供应链问题。
[参考文献]
[1]Ghadimi P,Wang C,Lim K M.Sustainable supply chain modeling and analysis:Past debate,present problems and future challenges[J].Resources,Conservation Recycling,2019,140:72-84.
[2]Georgiadis P,Besiou M.Environmental and economical sustainability of WEEE closed-loop supply chains with recycling:A system dynamics analysis[J].The International Journal of Advanced Manufacturing Technology,2010,47(5-8):475-493.
[3]Tordecilla R D,Juan A A,Montoya-Torres J R,et al.Simulation-optimization methods for designing and assessing resilient supply chain networks under uncertainty scenarios:A review[J].Simulation Modelling Practice and Theory,2020,106:102166.
[4]Namdar J,Li X,Sawhney R,et al.Supply chain resilience for single and multiple sourcing in the presence of disruption risks[J].International Journal of Production Research,2018,56(6):2339-2360.
[5]Merzifonluoglu Y.Risk averse supply portfolio selection with supply,demand and spot market volatility[J].Omega,2015,57.
[6]Maryam M,Ramin S.A multi-objective stochastic programming approach with untrusted suppliers for green supply chain design by uncertain demand,shortage,and transportation costs[J].Journal of Cleaner Production,2023,408.
[7]张英,魏明珠.基于鲁棒优化的逆向物流网络设计[J].物流工程与管理,2010,32(11):60-62.
[8]Zetina A C,Contreras I,Cordeau J,et al.Robust uncapacitated hub location[J].Transportation Research Part B,2017,106:393-410.
[9]Hossein Mirzaee,Hamed Samarghandi,Keith Willoughby.Arobust optimization model for green supplier selection and order allocation in a closed-loop supply chain considering Applications,2023,228.
[10]Alavi H S,Jabbarzadeh A.Supply chain network design using trade credit and bank credit:A robust optimization model with real world application[J].Computers Industrial Engineering,2018,125:69-86.
[11]Cecil A,Claver D,Uday V,et al.Distributionally robust optimization of a Canadian healthcare supply chain to enhance resilience during the COVID-19 pandemic[J].Computers Industrial Engineering,2022,168:108051.
[12]张玲,李锦棚,高妙仙.基于均值-CVaR的灾后临时献血点选址分布式鲁棒优化方案研究[J].福州大学学报(哲学社会科学版),2022(04):63-71.
[13]张玲,李锦棚,陈圣群.基于数据驱动的应急血液供应网络配置分布式鲁棒优化方案研究[J/OL].中国管理科学,1-11[2024-01-13].
[14]Zhang P,Liu Y,Yang G,et al.A distributionally robust optimisation model for last mile relief network under mixed transport[J].International Journal of Production Research,2022,60(4):1316-1340.
[15]Wang S,Chen Z,Liu T.Distributionally robust hub location[J].Transportation Science,2020,54(5):1189-1210.
[16]Cavus O,Kocaman A S,Yilmaz O.A risk-averse approach for the planning of a hybrid energy system with conventional hydropower[J].Computers&Operations Research,2021,126.
[17]Dixit V,Verma P,Tiwari K M.Assessment of pre and post-disaster supply chain resilience based on network structural parameters with CVaR as a risk measure[J].International Journal of Production Economics,2020,227(C):107655.
[18]Liangyan Tao,Sifeng Liu,Naiming Xie,et al.Optimal position of supply chain delivery window with risk-averse suppliers:A CVaR optimization approach[J].International Journal of Production Economics,2021,232:107989.
[19]Esfahani M P,Kuhn D.Data-driven distributionally robust optimization using the Wasserstein metric:Performance guarantees and tractable reformulations[J].Mathematical Programming,2018,171(1-2):115-166.
[20]Rui G,Anton K.Distributionally robust stochastic optimization with Wasserstein distance[J].Mathematics of Operations Research,2022,48(2):603-655.
[21]Daniel Zhuoyu Long,Melvyn Sim,Minglong Zhou.Robust satisficing[J].Operations Research,2022,71(1):61-82.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/78027.html