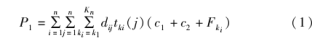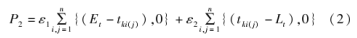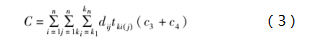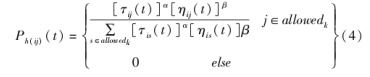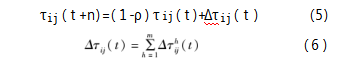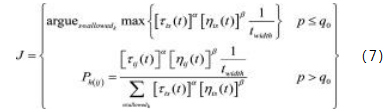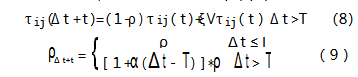【摘要】近年来,大数据云计算技术、人工智能算法被引入生鲜冷链物流配送管理中,可针对冷链物流的制冷成本、运输成本、时间窗惩罚成本使用蚁群优化算法(Ant Colony Optimization,ACO)、人工鱼群算法(Whale Optimization Algorithm,WOA),全面分析多点配送的带模糊工作时间窗的冷链物流最优配送方案。为保证生鲜肉品冷链配送低碳保鲜效益、运输成本效益的最优化,引入改进传统蚁群算法的种群初始化、转移状态规则、信息素调整因子PAF、信息素更新策略等方式,进行生鲜肉品冷链配送行进路线的粒子群寻优、迭代任务分配及迭代结果优化分析,得出更适合生鲜肉品企业冷链配送的最短路径。仿真实验结果显示,基于改进蚁群算法的冷链配送路径优化,相比蚁群优化算法等算法的寻优路线更优、保鲜及运输成本更低,能够产生更优良的冷链物流配送经济效益。
【关键词】生鲜肉品,冷链配送,最短路径,改进蚁群算法
互联网电子商务产业发展模式的网络化、高效化、低成本化,对商务运营网络结算、产品打包、冷链配送等各个交易环节提出更高的要求,使用大数据遗传算法作出冷链配送运输路线的种群初始化、寻优迭代分析成为企业降本提效的关键。刘琳,贾鹏等认为生鲜农产品的配送路径选择本质上属于车辆路径寻优问题(Vehicle Routing Problem,VRP),即针对在软性时间窗制约条件下如何选择最优的冷链保鲜方式、物流配送路径问题,提出多中心选址的冷链配送路径优化方案;吴志勇,戴弌等围绕人工鱼群算法建立多目标、多约束的冷链配送模型,结合变邻域搜索算法作出种群初始化、粒子群迭代收敛。基于以上人工鱼群遗传算法、可变邻域搜索算法等的研究,面向冷链配送的高保鲜度、高效率及低成本要求,建构以改进蚁群算法为主的冷链物流运输优化模型,求解多点配送的冷链车辆调度、最短路径寻优问题,提高生鲜肉品冷链配送的效率及服务管理质量。
1基于多指标要素约束的冷链物流配送运输优化模型建构
1.1问题描述
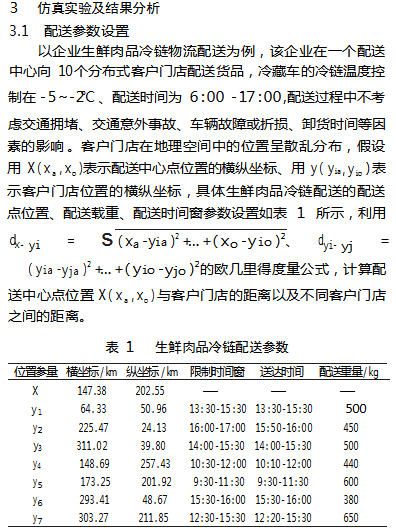
生鲜肉品的冷链配送是由1个配送中心发往多个客户门店,且配送中心、客户门店的地理位置保持固定,研究在封闭式道路环境、车辆载重一定情形下的冷链配送优化方案。假设冷藏车的生鲜肉品载重、物品冷藏包装方式、运输行驶速度保持恒定,按照规划路线在约定的时间窗内将特定物品配送至客户门店,为降低生鲜肉品配送过程中的腐坏变质率,采用蓄冷温控箱的冷链保存方式进行包装配送[1]。
基本假设条件为:①已知配送中心、每个客户门店的地理位置坐标,配送中心与客户门店的距离保持固定。②在符合车辆载重要求的情况下,冷藏车的生鲜肉品配送不考虑交通拥堵、交通意外事故、车辆故障或折损、卸货时间等无关因素。③生鲜肉品运送需在特定时间内送达客户门店,且配送路线不重复,超时则会被拒收。④冷藏车冷链配送的运输行驶速度、物品冷藏包装方式、冷藏温度保持恒定。⑤冷链配送方案的总行驶路程不超过配送车辆的最大续航行程。
1.2冷链配送模型建构
1.2.1参数说明
为便于冷链物流配送模型分析,选用X表示配送中心点位置,Y={y1,y2,…,yn}表示多个客户门店位置,dij表示yi到yj客户门店之间的距离;K表示冷藏车的集合K={k1,k2,…,kn},v表示冷藏车冷链运输的固定行驶速度,Q表示冷藏车的最大承载量,G表示冷藏车装载的冷链生鲜肉品重量。c1表示冷链运输过程中的单位时间内制冷成本,c2表示冷链运输前车厢单位时间的预冷成本,c3表示冷链运输单位时间内的人工成本,c4表示冷链运输单位时间内的油耗成本;tki(j)表示冷藏车ki到达客户门店yj的时间点,tij表示冷链配送从yi到yj客户门店位置的所用时间,ε1和ε2分别表示冷链物流配送早到、晚到客户门店的惩罚系数,[Et,Lt]表示冷藏车冷链运输配送的服务时间窗。Fki表示单位时间内冷藏车ki的冷链运输配送使用成本。
冷藏车ki将生鲜肉品配送至yj客户门店的单次配送成本可表示为式(1):
冷藏车ki将生鲜肉品配送至yj客户门店的时间窗惩罚成本可表示为式(2):
冷藏车ki将生鲜肉品配送至yj客户门店的固定费用成本可表示为式(3):
2基于改进蚁群算法的生鲜肉品冷链配送路径优化方案设计
生鲜肉品冷链配送的最短路径选择配置,本质上是车辆路径的非确定性多项式(NP-hard)寻优问题,即在存在多个道路节点、配送客户门店点情形下,在冷藏车最大承载量、冷藏车行驶速度、配送点位置、配送时间窗等条件因素的约束下,如何选择更为简短、快捷的最优路线进行货物配送,使其达成冷链配送成本花费最小、行驶路径最短的目标[2]。
2.1传统蚁群遗传算法
由意大利学者ColorniA提出的蚁群遗传算法,是以蚂蚁群落的觅食活动为依据,设置涵盖蚂蚁群、信息素、信息素浓度等要素的蚁群寻优算法,通过爬行蚂蚁识别路径中的信息素浓度来选择行进方向,利用轮盘赌法选择下一需要访问的路径节点,信息素浓度越高方向形成的正向反馈越强,随着时间推移蚁群会跟随前方蚂蚁找到最短的行进路径[3]。
假设M只蚂蚁沿着N个网络节点爬行且M={m1,m2,…,mn},蚁群算法寻优的信息素浓度为τij,不同网络节点的所有路径在初始阶段存在着同等的信息素浓度,蚂蚁通常会根据之前蚁群留下的信息素浓度来选择后续的爬行节点,则t时刻第h只蚂蚁选择从网络节点i爬行到j的概率可表示为式(4):
Ph(ij)(t)表示t时刻第h只蚂蚁选择爬行路径(i,j)的概率;τij表示(i,j)路径中所存在的信息素浓度,τis表示蚂蚁后续可选择爬行路径的总信息素浓度;ηij表示蚂蚁选择yi爬行到yj的期望程度,ηis表示蚂蚁后续可选择爬行路径的总期望程度;s∈allowedk表示第h只蚂蚁可选择的下一个且没有访问过的网络节点集合;α和β分别表示蚁群遗传算法的信息素权衡因子和期望值启发式因子。在蚁群完成所有网络节点的爬行寻找后,更新各节点路径的信息素浓度,其中,第h只蚂蚁在(i,j)路径中留下的信息素浓度可表示为Vτij(t)、蚁群爬行结束后(i,j)路径中留下的总信息素浓度可表示为τij(t+n),蚁群更新循环中的所有路径组成路径迭代的最优集合(TSP),具体计算公式如式(5)(6)所示。
其中,ρ和(1-ρ)分别表示信息素挥发因子、信息素留存因子,且ρ∈(0,1),在单个蚁群循环周期内使用轮盘赌法更新不同路径的信息素浓度,输出循环结束的最优路径,整个蚁群遗传算法的执行流程如下[4]。
①初始化种群参数。设定最大蚁群路径寻优的迭代次数为500次,在刚开始时设置当前时间t=0、迭代次数NC=0,初始阶段所有路径的信息素浓度均为0,根据蚂蚁路径行进的状态为信息素权衡因子α、期望值启发式因子β和信息素浓度τij赋值。
②将M只蚂蚁随机放置到不同的网络节点,使用Tabu Tablek禁忌表记录蚂蚁行走过的网络节点。
③根据Ph(ij)(t)的概率选择公式确定第h只蚂蚁的行走路径,计算t时刻第h只蚂蚁选择从网络节点i爬行到j的概率,更新TabuTablek禁忌表中allowedk网络节点集合的数量,将已访问过的网络节点从表中删除。
④判定第k只蚂蚁是否完成单次的路径寻找循环,若为“否”则返回第三步进行重新执行,否则进入下一步。
⑤根据计算公式(5)(6)作出全局信息素浓度更新,并判定算法是否达到迭代次数,若“是”则结束算法循环、输出最终的路径寻优结果,否则返回第三步继续执行。
2.2改进蚁群遗传算法设计
传统蚁群算法经过空间内多次信息素跟随的路径寻优后,通常会在某一最优路径中存留更高的信息素浓度,导致后续蚂蚁群选择某一路径的概率几乎不发生变化,也即全部向着信息素浓度最高、寻优次数最多的路径方向爬行,导致算法陷入局部最优解,因而需通过设置状态转移规则、信息素浓度更新策略的改进来解决这一问题[5]。
①状态转移规则。当前改进蚁群遗传算法中蚂蚁路径寻优的下一网络节点选择,通常围绕着路径(i,j)的信息素浓度、选择下一节点J的等待时长twait、节点J的时间窗宽度twidth进行展开。假设在全局范围内,蚂蚁h从网络节点i爬行到j选择最优路径的概率值为q0,选择非最优路径的概率值为p,则在引入节点J的等待时长twait、节点J的时间窗宽度twidth等时间窗因子后,可依据最优路径的概率值q0设定伪随机搜索的比例选择规则,按照式(7)作出下一路径的选择操作。
J表示蚂蚁h选择从网络节点i爬行到j节点的概率值,q0表示选择最优路径的概率值,p表示选择非最优路径的概率值;twidth表示节点j的时间窗宽度,s∈allowedk表示第h只蚂蚁可选择的下一个、且没有访问过的网络节点集合。在p>q0情形下,使用伪随机搜索的比例选择规则作出蚂蚁行进路径的状态转移计算:选择r=[0,1]的伪随机数,伪随机数r为均匀变化的常量,在r<p(1)情况下选择第1只蚂蚁进行路径寻优计算,否则,选择第h只蚂蚁作出路径寻优计算,并且使p(h-1)<r≤p(h),通过这种方式可完成对最优路径dq0以外的其余路径dp的寻优计算,实现全局范围内蚁群行进路径的选择求解[6]。
②改进信息素浓度的更新策略。在蚂蚁路径寻优的循环周期内,路径信息素浓度的大小很大程度上影响着最优路径搜索的质量,由于部分网络节点的信息素浓度较低、信息素挥发因子ρ数值较大,使其很难出现在蚁群寻优搜索的范围内,而那些信息素浓度高、信息素挥发因子ρ数值较小的网络节点则长期存在于蚁群搜索的范围内,由此,蚁群路径搜索陷入局部最优解。
为解决这一问题,需基于蚂蚁周期系统(Ant-CycleSystem)调整不同路径中的信息素浓度、信息素挥发因子值,引入距上次最优解经过的时间T、T时刻多次迭代后的网络节点O,也即在T时刻对现有的信息素浓度、信息素挥发因子更新策略作出改进,设定“第h只蚂蚁选择(i,j)路径的配送总成本若小于所有蚂蚁参与配送的平均总成本,则该路径信息素浓度增加,否则信息素浓度减少”的更新策略,作出蚂蚁路径选择的全局寻优搜索,具体计算公式如式(8)(9)。
其中,Δt表示蚂蚁路径寻优经过的实际时间,T表示距上次最优解经过的时间;τij(Δt+t)表示在Δt+t时刻蚂蚁寻优的路径的信息素浓度值,ξ表示信息素浓度的可调节系数;α表示信息素权衡因子,ρΔt+t表示在Δt+t时刻蚂蚁寻优的路径的信息素挥发因子数值。从以上式(8)(9)可以得出,ξ会随着Δτij(t)值的增加而减小,也即在某一蚂蚁行走路径的总信息素浓度值不断增加时,ξ的可调节系数会逐渐减小,以此控制该条路径中总信息素浓度值继续增大,避免使蚁群路径搜索陷入局部最优解;在蚂蚁路径寻优经过的实际时间小于T时,蚂蚁寻优的路径的信息素挥发因子不改变,但当Δt>T时,表明蚂蚁路径寻优经过的实际时间过长,则此时基于式(9)可增大蚂蚁寻优路径的信息素挥发因子数值,加强路径中信息素浓度的挥发,避免蚁群路径搜索陷入局部最优解。
3.2实验结果分析
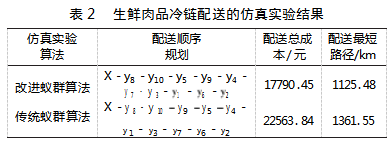
基于改进蚁群算法进行××企业生鲜肉品冷链配送的路径寻优实验,设定信息素权衡因子α=2.0、期望值启发式因子β=4.0、信息素挥发因子ρ=0.5、控制转移规则的伪随机数r=0.5,设置改进蚁群算法最大迭代次数为500次,距上次最优解经过的时间T=1 min、信息素浓度的可调节系数控制在 [-1,1]的变化范围内。基于MATLAB R2022a仿真实验软件,通过公式(7)(8)(9)作出模型收敛性、可靠性的仿真分析,得到如表2所示的仿真实验结果。
从表2可发现,在满足生鲜肉品冷链配送时间窗要求的情况下,改进蚁群算法选择X-y8-y10-y5-y9-y4-y7-y3-y1-y6-y2的配送路线更加合理,配送总成本为17790.45元、配送最短路径为1125.48km,相比传统蚁群算法的生鲜肉品冷链配送路径选择更优,VRP车辆路径问题求解中能够得到更优的配送方案、更短的配送路径,可满足生鲜肉品冷链配送的实际需求。
4结语
在时间窗、配送总成本约束条件下,使用改进传统蚁群算法作出生鲜肉品冷链配送最短路径寻优,相比其他算法而言能够避免陷入局部最优迭代、增加邻域结构的多样性,根据以上仿真实验结果得出,基于改进蚁群算法的生鲜肉品冷链配送种群迭代的最短路径更短、运输及保鲜成本更低,可有效提升企业冷链物流配送的效率及经济效益。
[参考文献]
[1]刘琳,贾鹏,高犇,赵雪婷.新鲜度限制约束下物流配送中心选址-路径优化[J].包装工程,2022(05):232-241.
[2]李想,闵德权,张祺.随机需求下半开放式冷链物流车辆路径优化[J].包装工程,2022(07):160-169.
[3]吴志勇,戴弌,鞠传香,胡本佳,胡啸.基于鲸鱼优化算法的多目标多式联运路径选择[J].重庆交通大学学报(自然科学版),2022(05).
[4]鲍惠芳,方杰,张进思,王传胜.基于改进蚁群算法的低碳冷链配送路径优化[J].系统仿真学报,2024(01):183-194.
[5]邓忆瑞,郑瑶,姜明月,徐小峰.带模糊工作时间窗的多配送中心同时集散货物车辆路径问题[J].管理评论,2022(10):258-269.
[6]胡蓉,陈文博,钱斌,郭宁,向凤红.学习型蚁群算法求解绿色多车场车辆路径问题[J].系统仿真学报,2021(09):2095-2108.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/78025.html