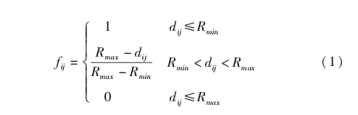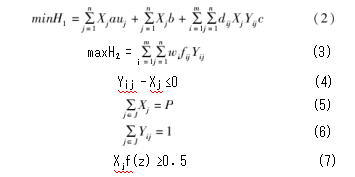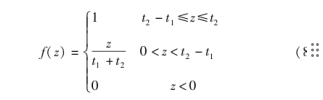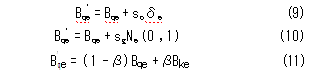基于两阶段法的地铁货物运输中转点选址研究论文

　　【关键词】选址问题,两阶段法,地铁货运,层次分析法,并行突变免疫算法

        城市货物运输的快速发展，使得地面交通面临巨大挑战。但地铁夜间不进行客运，且非高峰时有较大的空余，造成大量运能浪费。考虑利用地铁剩余运能进行城市货物运输，不仅能充分利用地铁时空资源，还能提高地面交通的流畅性，减少交通拥堵。因此，构建地上－地下一体化货物运输体系是十分必要的。

        地铁货物运输中转站是地铁货物运输系统的关键节点，其位置决定地铁货物运输的规模。大多数学者利用双层规划模型的层次性特点研究地铁货物运输中转站选址[2-4]。多目标、单目标数学模型也适用于地铁货物运输中转点选址，但模型的求解算法存在差异。张秋星[5]通过地铁站节点综合重要度评价模型，筛选出中转站的备选点，通过成本模型，求解出相应的中转站。陈徽[6]设计出混合智能算法，以求解运输成本最小化的多阶段货运站选址模型。王苏林等[7]建立了以物流节点数量最少及物流节点转运率最低为目的的双层多目标规划模型，并结合贪心算法和遗传算法进行优化求解。戚建国等[8]构建了以极小化旅客旅行时间和未满足货物惩罚成本为目标的混合整数线性规划模型。随着地铁货物运输中转站选址研究的深入，有学者提出结合路径问题来研究选址问题。周芳汀等[9]提出基于地铁配送的选点－路径问题，以最小化货物平均送达时间为目标，利用改进递归粒度算法，求解配送中心以及配送路径的选择。任睿等[10]建立熵权-TOPSIS模型筛选地下货运流量；考虑设施容量约束，以建设运营成本为目标，构建网络选址－分配－路径组合优化模型。

 

　　已有的研究中，关于中转站选址问题的定量、定性分析法已经趋于成熟，但定性分析的主观性较强；定量分析的结果更为直观、简洁、准确，应用效果好，但操作具有局限性。因此，结合定性分析与定量分析的优势，使地铁货物运输中转站的选址问题在准确性和完备性上相互补足，本文建立基于两阶段法的城市地铁货物运输中转站选址模型。第一阶段充分考虑既有地铁站点各种因素，利用层次分析法构建地铁货物运输备用中转站的选址模型，筛选出地铁货物运输备用中转站的位置。第二阶段构建考虑乘客舒适度的成本最小、覆盖率最大的多目标优化模型，并利用改进的并行突变免疫算法求解，得到地铁货物运输中转站最优选址位置。
 

　　１中转站选址模型建立
 

　　地铁货物运输中转站是地铁货物运输网络中用于货物临时存放处理并完成转运输送功能的节点。中转站设立的目的是减轻货物运输的压力，实现分流运输。
 

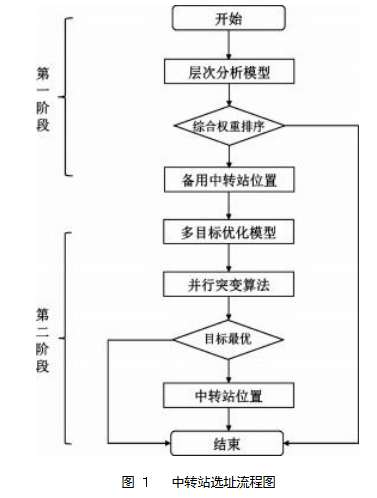
　　两阶段法是将规划问题划分为两个阶段去求解：第一阶段是得到初始基本可行解，即通过层次分析法在既有地铁站中筛选出地铁货物运输备用中转站。第二阶段在初始基本可行解的基础上进一步求解，即在地铁货物运输备用中转站的基础上找到最适合的地铁货物运输中转站。本文基于两阶段的思路，建立地铁货物运输中转站的选址模型。地铁货物运输中转站选址流程图如图１所示。

 

　　２基于两阶段法的地铁货运中转站选址

       ２．１第一阶段—备用中转站的选择
 

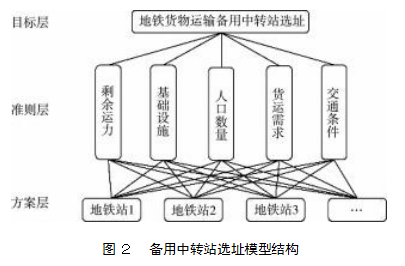
　　备用中转站的选择需要综合、全面地考虑各种因素，因此选用层次分析法较为适合。层次分析法是一种定性和定量相结合的系统化、层次化的分析方法［１１］。地铁货物运输备用中转站选址模型结构如图２所示。目标层为在既有地铁站的基础上筛选出地铁货物运输备用中转站。准则层的五个指标分别为地铁列车车厢的剩余运力、地铁站周边的人口数量、地铁站的基础设施、地铁站周边货物运输需求、地铁站周边道路交通条件。其中，地铁列车车厢的剩余运力是进行地铁货物运输中转备用站选址最关键的因素；只有在满足客运需求的前提下，才能考虑利用地铁进行货物运输。方案层则由既有地铁站点组成。

 

　　传统的层次分析法通常采用 １ －９ 标度法，但其一致性较差，因此，考虑采用１－７分数标度法。１－７分数标度法如表１所示。

 

　　２．２第二阶段—中转站的确定
 

　　尽管层次分析法是定量分析与定性分析的结合，但定量数据较少，定性成分多，不易令人信服。而多目标优化模型针对地铁货物运输中转站成本、距离、剩余运力最小化的特点，可以生成多个不同的解决方案。因此，在两阶段法的第二阶段利用多目标优化模型，定量分析地铁货物运输备用中转站位置，选择满足目标函数的最优地铁货物运输中转站位置。
 

　　２．２．１问题描述
 

　　在地铁既有站的基础上，通过层次分析法筛选出ｎ个地铁货物运输备用中转站，集合为Ｊ＝（１，２，３，…，ｎ）；地铁线路周围分布ｍ个客户需求点，集合为Ｉ＝（１，２，３，…，ｍ）。目标为在地铁货物备用中转站的基础上筛选出地铁货物运输中转站，使得Ｉ个客户需求点尽可能被覆盖，并且要求筛选出的地铁货物运输中转站建设成本、中转成本、配送成本最小。假设每个客户需求点ｉ只可以由一个地铁货物运输中转站ｊ提供服务；客户需求点的位置是固定不变的；地铁货物运输中转站对客户需求点覆盖率变化采用线性函数表示，如式（１）所示。

 

　　其中，fij表示随着距离变化的覆盖度函数；dij为需求点i到备用中转站j的直线距离；Rmax表示最大半径，Rmin表示最小半径。
 

　　2.2.2参数说明
 

　　Xj和Yij为决策变量。其中，Xj为是否选择在j备用站建立中转站，若在j备用站建立中转站，则Xj=1,否则Xj=0;Yij为需求点i是否由j中转站服务，若需求点i由j中转站服务，则Yij=1,否则Yij=0。a为单个备用中转站的改建成本。uj表示备用中转站需要改建程度系数。b为单个备用中转站的中转成本。c为单位距离配送成本。w i为需求点的权重。f(z)表示乘客的舒适度，乘客的舒适度取决于地铁的剩余运力。
 

　　2.2.3目标函数

 

　   式(2)表示中转站的总成本最小；式(3)表示中转站的总覆盖率最大化；式(4)表示只有在j设立中转站时，客户需求点i被中转站j服务；式(5)表示需要建立P个地铁货物运输中转站；式(6)表示每个客户需求点只能由一个中转站服务；式(7)表示地铁货物运输的前提是满足乘客舒适度，乘客的舒适度会随着地铁剩余运力的增加而增加，f(z)的函数表达式如式(8)所示：

 

　　式中，z表示单位时间单位断面剩余运力；t1表示单位时间单位断面坐客载荷（人次）；t2表示单位时间单位断面定员载荷（人次）。
 

　　2.2.4模型求解
 

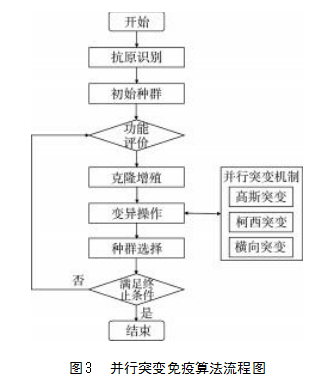
　　免疫算法是将免疫概念和免疫理论应用于遗传算法的一种算法，是遗传算法的延申。由于传统算法的随机搜索特性，免疫算法仍然存在收敛速度慢和局部极小值捕获问题的弊端。为提高算法的收敛速度和求解质量，本文采用一种改进的并行突变免疫算法[12]。并行突变免疫算法流程图如图3所示，其中功能评价步骤的内容为传统免疫算法中的亲和度评价、抗体浓度评价、激励度评价。

 

　　相较于免疫算法，并行突变算法的创新点是在不同的条件下选择三种突变算子，分别为柯西突变产生的算子、高斯突变产生的算子以及横向突变产生的算子。三种突变算子的实现公式如下：

 

　　式(9)为柯西实现公式，其中群体的序列号由符号q表示，维度由符号e表示，s c表示柯西突变步长，δe表示柯西随机变量；式(10)为高斯实现公式，sg表示高斯突变步长，Ne(0,1)表示正态分布的高斯随机数；式(11)为横向实现公式，β是随机生成的实数，且k≠q。
 

　　对比三种突变算子得到：高斯变异的局部搜索能力较好，但是引导个体跳出局部较优解的能力较弱，不利于全局收敛；柯西突变算子能够增加种群的多样性，提高算法的全局搜索能力，增加搜索空间；横向突变算子的收敛速度快。
 

　　并行突变算法还改进了两种突变算子的学习概率设置策略：①每个突变算子的概率相等。②基于亲和力的规则确定概率，并进行归一化处理。突变算子的学习概率计算式如下：

 

　　式(12)表示三种突变算子的学习概率之和为1,ProbCM表示柯西突变算子的学习概率，ProbGM表示高斯突变算子的学习概率，ProbLM表示横向突变算子的学习概率；式(13)-式(15)分别为三种突变算子的学习概率计算公式，t表示当前迭代次数，Tmax表示最大迭代次数。
 

　　3算例分析
 

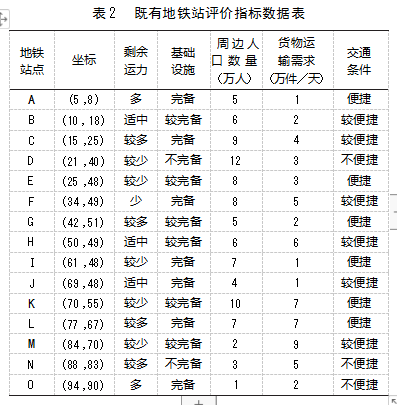
　　以单一地铁线路为例，进行地铁货物运输中转站选址研究。其中，线路上有15个地铁站点，客户需求点随机分布在地铁线路两侧。既有地铁站评价指标数据如表2所示。

 

　

　　3.1第一阶段—备用中转站的选择
 

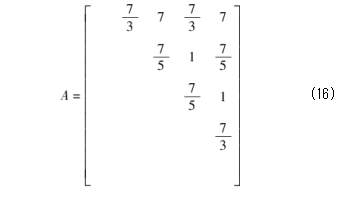
　　通过层次分析模型，计算五个评价指标的权重系数，即在备用中转站选址中的重要程度。选用上三角构造判断矩阵，能在减少一半工作量的同时，更好地满足矩阵完全一致性的要求。因此，通过专家打分和问卷调查的方法，得到剩余运力、周边人口数量、基础设施、货物运输需求以及交通条件的判断矩阵，如式(16)所示。

　　
 

　　利用算术平均法计算得到w=(0.4860 0.1544 0.1172 0.1567 0.0857);用原始矩阵A乘以w,得到Aw=(2.6325 0.8035 0.6019 0.8031 0.4497)T;最大特征值的计算公式为：

　
 

　　通过式(18)计算得到矩阵A不一致程度的指标CI≈0.0564.

　
 

　　其中，CR表示一致性比率；CI表示不一致程度指标；RI表示平均一致性指标，当n=5时，RI=1.12;通过式(18)计算得到CR≈0.0503<0.1,因此，通过一致性检验，可认为判断矩阵计算出的权重值合理，各个指标的权重如表3所示。
 

　
 

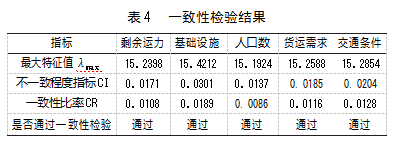
　　根据表2中各个站点的各项指标，分别计算剩余运力、周边人口数量、基础设施、货物运输需求以及交通条件的权重w、最大特征值λmax、不一致程度指标CI以及一致性比率CR,并排出优劣顺序；其中，查找一致性检验RI指标表可知，当n=15时，RI的值为1.59。利用Matlab计算得到各评价指标权重与一致性检验结果，如表4所示。

 

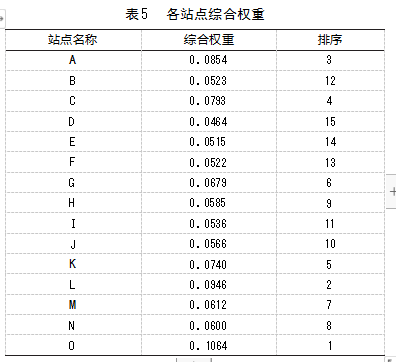
　　计算得到各个方案的准则层不同指标的权重后，利用加权求和的方法，计算各个方案的综合权重，各站点综合权重如表5所示。其中：O站点的综合权重最大，为0.1064;D站点的综合权重最小，为0.0464。在15个地铁站点中选取7个站点作为地铁货物运输备选中转站，分别为A站点、C站点、G站点、K站点、L站点、M站点、O站点。

 

　　3.2第二阶段—中转站的确定
 

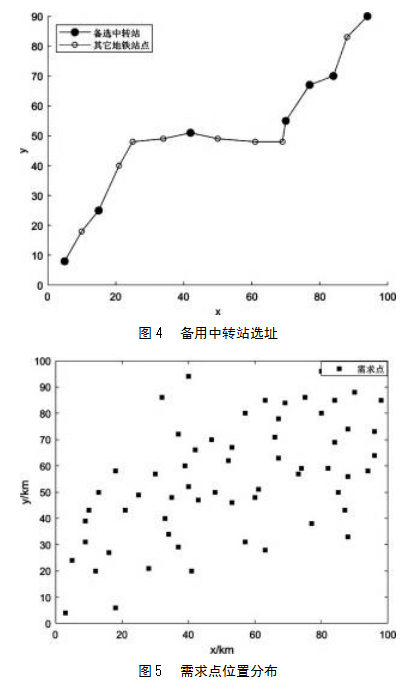
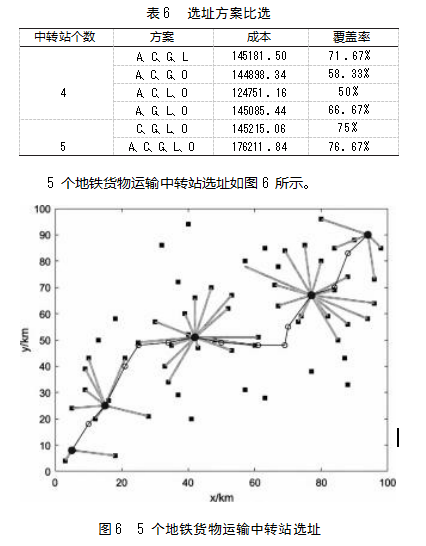
　　通过层次分析模型在既有地铁站中选出7个地铁货物运输备用中转站，备用中转站选址如图4所示。假设有60个需求点，需求点位置分布如图5所示。

 

　　假设单个备用中转站的改建成本a为100000元／个；备用中转站需要改建程度uj与地铁站基础设施相关，完备对应的改建程度系数为0.3,较完备对应的改建程度系数为0.5,不完备对应的改建程度系数为0.7;中转成本b为1000元／个；单位距离配送成本c为2元／次；需求点i的权重w i与货物运输需求数量成正比，假定每个需求点的货物运输数量相同；中转站最大覆盖半径Rmax为20公里，最小覆盖半径Rmin为10公里。利用Matlab对并行突变免疫算法编程，求出满足多目标优化模型的地铁货物运输中转位置。并行突变免疫算法的参数设置：种群规模为50;恒定的克隆大小为10;迭代次数为100。
 

　　通过计算得到选址方案比较结果，选址方案比选如表6所示；在有约束条件的限制下，当地铁货物运输中转站的个数为4个时，共有五个方案。其中，如果只考虑成本，选择A、C、L、O四个站点作为地铁货物运输中转站，成本为124751.16元；如果只考虑覆盖率，选择A、C、G、L四个站点作为地铁货物运输中转站，覆盖率为71.67%。当地铁货物运输站中转站的个数为5个时，仅有A、C、G、L、O方案可选，该方案的成本是176211.84元，覆盖率为76.67%。

　
 

　　4结论
 

　　地铁货物运输有助于提高货物运输效率、缓解城市道路交通压力，因此，针对地铁货物运输中转站选址的研究尤为重要。本文通过研究得到以下结论：
 

　　①基于两阶段法的城市地铁货物运输中转站选址模型的建立，不仅突出地铁进行货物运输的特点是在剩余运能足够的前提下，还能定性定量地分析选址问题。通过某地铁线路为例，验证了该模型的可行性与有效性。
 

　　②第二阶段多目标优化模型充分考虑改建成本、转运成本、配送成本以及覆盖率构建目标函数，在客户舒适度等约束条件下，利用并行突变免疫算法求解多目标模型，提高搜索范围和求解速率，使结果更加符合实际。
 

　　③通过对比发现，地铁货物运输中转站的数量不同，最优选址方案不同；目标的侧重点不同，最优选址方案不同。
 

　　［参考文献］
 

　　[1]胡万杰，董建军，陈志龙．基于地铁货运系统的城市物流发展模式探讨[J].铁道运输与经济，2022,44(02):8-15.
 

　　[2]李晓迪．城市地下物流系统节点选址研究[D].马鞍山：安徽工业大学，2021.
 

　　[3]刘一凡，董岗．中欧班列集结中心选址优化研究[J].铁道运输与经济，2023,45(10):10-18.

       [4]王曼，曹倩，孙践知，等．地下物流多级节点选址的双层规划模型[J].科学技术与工程，2018,18(31):64-69.
 

　　[5]张秋星．基于地铁运输系统的城市配送中心选址研究[D].北京：北京邮电大学，2022.
 

　　[6]陈徽．基于既有站的铁路货运站选址研究[D].北京：北京交通大学，2021.
 

　　[7]王苏林，邱菲尔，陈凡，等．基于贪心遗传的地下物流节点选择规划研究[J].工业工程，2020,23(05):88-95.
 

　　[8]戚建国，周亚茹；杨立兴，等．客货共运模式下高铁列车货运兼办方案优化[J].北京交通大学学报，2023,47(04):1-11.
 

　　[9]周芳汀，周国华，张锦．依托地铁网络的城市配送系统转运点选址研究[J].铁道学报，2019,41(07):16-25.

       [10]任睿，胡万杰，董建军，等．轴辐式城市地铁－货运系统网络布局优化[J].系统仿真学报，2021,33(07):1699-1712.

       [11]李彦，朱吉胜．层次分析法的一种改进及其应用[J].电子设计工程，2011,19(15):29-31+35.
 

　　[12]Lulu L,Shuaiqun W.An improved immune algorithm with parallel mutation and its application[J].Mathematical Biosciences and Engineering,2023,20(7):12211-12239.