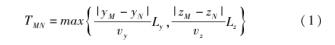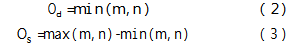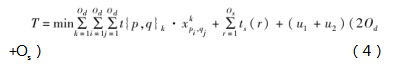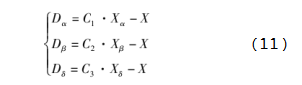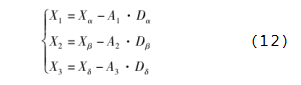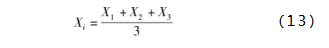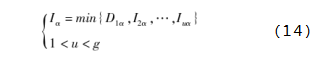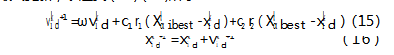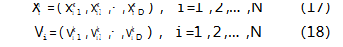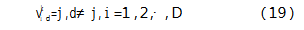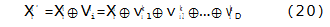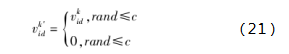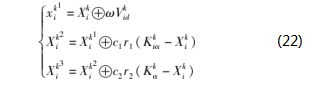基于 GWO - PSO 算法的堆垛机混合作业优化研究论文

　　【关键词】混合作业,灰狼优化算法,粒子群优化
 

　　Research on Mixed Operation Optimization of Piler Based on GWO-PSO Algorithm
 

　　【Abstract】In order to reduce the running time of the mixed operation of the piler,the mathematical model of the minimum running time of the piler is established,and an improved GWO-PSO algorithm is proposed to solve it.Firstly,in the initialization stage,grey wolves are randomly divided into several groups,and the leader,wolf king,is selected for independent optimization according to the standard GWO algorithm.Secondly,the position update mode of the PSO algorithm is used to update the optimization results to ensure the diversity of the population and the optimization speed of the algorithm.Thirdly,the velocity exchange operator is introduced for discretization,and the problem that the algorithm is easy to fall into local optimal is solved by setting the threshold value.Finally,the effectiveness of the GWO-PSO algorithm is verified by an example simulation.

       【Key words】mixed operation;grey wolf optimization algorithm;particle swarm optimization algorithm

       1引言
 

　　针对自动化立体仓库中堆垛机的发展，目前研究方向主要分为系统建模和优化控制两方面。
 

　　Malmborg,Krishnakumar[1]针对自动化立体仓库进行建模，根据作业特点建立了单指令与多指令作业的数学模型，为仓库的优化设计提供了理论指导。Wang等[2]以穿梭车和堆垛机组合执行存储和检索任务的仓储系统为研究对象，提出了一种基于穿梭车和堆垛机的运动时序数学模型，最大限度地减少了堆垛机的运行时间和穿梭时间。卞和营，方彦军[3]根据堆垛机的出入库作业方式，将高斯变异算子和贪心交叉算子引入遗传算法、粒子群算法进行求解，提高了全局搜索能力。Venkata,Gajendra[4]采用分支定界法求解货位优化非线性整数规划模型，一定程度上降低了作业效率和企业成本。林松森[5]提出了由PID、模糊PID以及免疫反馈三者组合的模糊免疫PID控制，将其应用于堆垛机控制系统的改进研究，并与原始PID控制效果进行比较，结果显示所设计的算法提高了堆垛机控制系统的稳定性和抗干扰性能。杨玮等[6]通过分析堆垛机和穿梭车的实际路径行程，提出了一种基于三维空间环境的改进混合蚁群算法来解决复合作业下的路径规划问题。程永强，汪岚[7]在最大最小蚁群算法的基础上，融合2-opt策略对局部进行优化，有效地解决了传统蚁群算法解决堆垛机调度问题的早熟情况。陈晨，茅健[8]把立体仓库堆垛机路径问题归结为旅行商问题，将传统蚁群算法与粒子群算法构建成混合算法，结果证明混合后的算法路径优化速度更快。Pan等[9]在建立货位分配模型时采用分类存储策略，以堆垛机拣选货物时间为目标，综合考虑其对出入库的影响。
 

　　Ｍａｔｅｊ等［１０］以堆垛机运行的耗能及仓库货物平均吞吐量为分配原则，建立仓库数学模型，并使用ＮＳＧＡ－ＩＩ得到最优解，为货物分配问题提供了新的思路。鄂晓征等［１１］建立了以堆垛机拣选效率和货架稳定性为货物分配原则的数学模型，运用权重系数法给予两种原则不同的比重，再采用遗传算法进行货位分配优化，取得了一定成效。汤洪涛等［１２］以堆垛机拣选效率为目标函数，提出Ｋ－Ｍｅｄｏｉｄｓ聚类的粒子群优化算法，提高了仓库拣选效率。
 

　　综上所述，智能优化算法常用于解决堆垛机优化问题，本文建立堆垛机运行时间最小的数学模型，并将ＧＷＯ算法和ＰＳＯ算法结合起来，形成ＧＷＯ－ＰＳＯ算法，解决了两个基本算法对种群初始化较为敏感、易过早收敛陷入局部最优解的问题。
 

　　２堆垛机混合作业时间优化数学模型

       ２．１堆垛机作业假设
 

　　由于每台堆垛机分管相邻共两排的货位，为更好地研究出入库策略，提出以下假设：
 

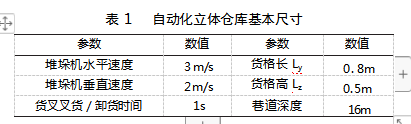
　　①每个货格只允许存储一个货物，所有货格尺寸相同，存放货物的体积小于仓库货位的容积，货格长Ｌｙ和Ｌｚ。
 

　　②堆垛机的出入库位置在同一侧，堆垛机的运行过程视为匀速运动，不考虑变加速时间，可同时在水平和垂直方向上运动，速度分别ｖｙ为和ｖｚ。
 

　　③在一组任务完成之后才会进入下一组任务，且任务之间不重叠。
 

　　④某一货物的位置可以用（ｘ，ｙ，ｚ）表示，代表该货物置于第ｘ排、第ｙ列、第ｚ层。
 

　　２．２堆垛机作业时间分析
 

　　根据以上假设，以某一堆垛机为例，由于其运行时间只受ｙ、ｚ坐标值的影响，因此该堆垛机从任意坐标点（ｙＭ、ｚＭ）运动到坐标点Ｎ（ｙＮ，ｚＮ）所需的时间可以用式（１）表示：

 

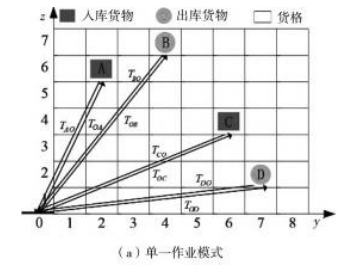
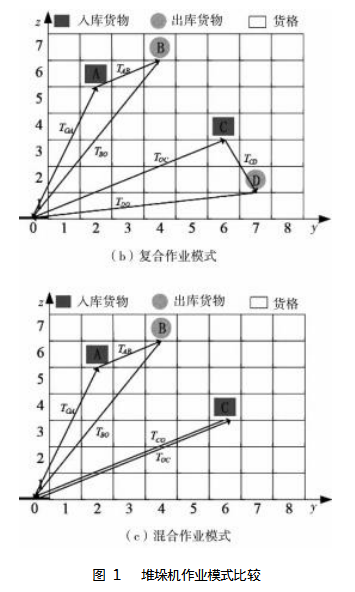
　　当出入库货物数量相等时，可以采用单一作业模式与复合作业模式；当出入库货物数量不相等时，可以采用单一作业模式和混合作业模式，各模式图解如图１所示，其中堆垛机出入库台坐标ｙ＝０，ｚ＝１。

 

       通过对堆垛机作业模式的分析可知，不同的作业顺序所造成的时间差最终反映在堆垛机空载作业时间差上。因此，可以通过对堆垛机作业时间优化使空载时间最小。
 

　　２．３堆垛机时间优化模型
 

　　为描述方便，设待处理任务为Ｒ＝｛Ｐ，Ｑ｝，其中Ｐ＝｛ｐ１，ｐ２，…，ｐｉ，…，ｐｍ｝，Ｐ表示待入库货物的集合，共ｍ件，Ｑ＝｛ｑ１，ｑ２，…，ｑｊ，…，ｑｎ｝，Ｑ表示待出库货物的集合，共ｎ件。这些待处理任务Ｒ最终形成Ｑｄ项复合作业任务和Ｑｓ项单一作业任务，其表达式如式（２）及式（３）所示：

　　
 

　　建立堆垛机拣选时间最小的数学模型，其目标函数如式（４）所示：

　　
 

　　该式表示堆垛机完成多项复合作业任务和单一作业任务所需的最小时间，式中，｛ｐ，ｑ｝ｋ表示第ｋ项复合作业任务，ｘｉ，ｑｊ为决策变量，表示第ｉ个待入库货物与序列扰动后的第ｊ个待出库货物一起被分配到第ｋ项复合作业，ｔｓ（ｒ）表示堆垛机在第ｒ项单一作业移动所需时间，ｕ１表示堆垛机叉货时间，ｕ２表示堆垛机卸货时间。

       约束条件：
 

　　堆垛机不能对同一货物进行重复作业，并保证每个货物只访问一次，使决策变量取值有效，表示为：

　

 

　　３改进的ＧＷＯ－ＰＳＯ算法

       ３．１ＧＷＯ－ＰＳＯ算法设计
 

　　２０１４年，澳大利亚学者Ｍｉｒｊａｌｉｌｉ等［１３］提出了一种群体智能算法，即灰狼优化算法。该算法将灰狼分为α狼、β狼、δ狼及ω狼，通过模拟狼群社会等级和集体狩猎行为的过程，实现对复杂问题的优化求解。１９９５年，由于受到鸟群捕食行为的启发，Ｋｅｎｎｅｄｙ，Ｅｂｅｒｈａｒｔ［１４］提出了一个简单的算法模型，经过多年的修改完善，最终形成了粒子群优化算法。
 

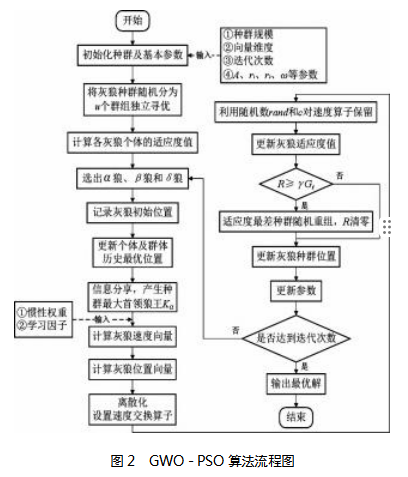
　　为避免种群过早收敛陷入局部最优，引入粒子群算法与灰狼优化算法进行结合优化，解决在初期的寻优多样性问题。在初始化阶段，将包含ｇ（ｇ∈Ｎ＋）个灰狼个体的种群随机分为ｕ（ｕ∈Ｎ＋）个群组，各群组按照标准灰狼优化算法独立进行猎物的寻找工作。
 

　　以某一群组为例，该群组首先包围猎物，追捕猎物的过程中，α狼、β狼和δ狼与ω狼之间的距离如式（１１）所示：

　
 

　　式中，Ｄα、Ｄβ和Ｄδ分别为当前α狼、β狼和δ狼与ω狼之间的距离，Ｘα、Ｘβ和Ｘδ分别为当前α狼、β狼和δ狼的位置，Ｃ１、Ｃ２和Ｃ３分别为对应当前α狼、β狼和δ狼的随机向量，Ｘ为当前灰狼个体的位置。

　　可以得出，ω狼向α狼、β狼和δ狼移动的方向和距离Ｘ１、Ｘ２和Ｘ３如式（１２）所示：

　　
 

　　在群组内，ω狼迭代更新的位置Ｘｉ用其向α狼、β狼和δ狼移动距离的平均数表示，如式（１３）所示：

　
 

　　此时，内部寻优结束，立即进行信息的共享，并推举产生种群的最大首领狼王Ｋα，其中Ｋα从各群组中的α狼中产生，其适应度值最小，表示为Ｉα，即模型目标函数值最小，对应最优位置表示为Ｘαｂｅｓｔ，Ｉα由式（１４）产生：

　　
 

　　式中，Ｉα为各种群的最大首领狼王的适应度值，Ｉｉα为各群组中最优的α狼的适应度值，对应该群组α狼最优位置Ｘαｉｂｅｓｔ，ｇ为灰狼个体数，ｕ为灰狼个体产生的粒子群组数。
 

　　由于各个灰狼群组中个体数量较少，在后期收敛时速度较慢，因此采用粒子群算法位置计算方法，来对ω狼进行位置最终更新，表达式（１５）（１６）所示：

　　
 

　　式中，ｋ为迭代次数；ω为权重惯性，是个体对自身运动的信任程度，ｃ１为群组学习因子，ｃ２为种群学习因子，ｒ１和ｒ２为［０，１］内的随机数，ｖｄ表示灰狼ｉ在第ｋ次迭代中第ｄ维的速度向量，ｘｄ表示灰狼ｉ在第ｋ次迭代中第ｄ维的位置向量，ｘｉｂｅｓｔ表示在第ｋ次迭代中适应度最优α狼的位置，Ｘｂｅｓｔ表示种群在第ｋ次迭代中适应度最优的狼王。
 

　　由于堆垛机出入库问题的解空间为离散域，需要对改进的ＧＷＯ－ＰＳＯ算法进行离散化处理，本文采用排列编码方式解决。假设第ｉ个灰狼个体位置为一个Ｄ维向量，在第ｋ次迭代中，其位置和速度分别表示为：

　　
 

　　设置速度交换算子ｖｄ进行个体位置的更新：

　
 

　　当ｊ≠０时，交换Ｘ中的ｘｄ和ｘ，若ｊ＝０则不进行操作。
 

　　综上，在速度交换算子ｖｄ的作用下，灰狼的个体更新如式（２０）所示。
 

　
 

　　式中，Ｘ′为在第ｋ次迭代后，第ｉ个灰狼个体的位置。
 

　　由上文可知，在改进ＧＷＯ－ＰＳＯ算法中，共包含Ｄ个速度交换算子，为避免计算量过大，利用随机数ｒａｎｄ（ｒａｎｄ∈［０，１］）和概率ｃ（ｃ∈［０，１］）来完成对每个分量速度交换算子进行保留，保留过程如式（２１）所示。

　　
 

　　式中，ｖ为分量速度交换算子在第ｋ次迭代后，第ｉ个灰狼的第ｄ维速度向量。当随机数ｒａｎｄ小于等于ｃ时，该分量速度交换算子保留，否则不保留。
 

　　经过一系列变换更新，GWO-PSO算法得到的新的位置计算公式如式(22)所示。

 

　　式中，X1、X2和X3分别为第k次迭代时，灰狼i位置的三次迭代，X3为最终迭代位置。
 

　　经过GWO-PSO算法的改进，通过狼王的指导，灰狼在位置更新时综合考虑了历史最优位置以及个体最优位置，保证了种群的多样性与群组的独立性。为了防止GWO-PSO算法陷入局部最优，引入随机重组阈值R对狼王适应度值进行标记，其表达式如式(23)所示：
 

　　R=γGt(23)
 

　　式中，γ为取值范围在(0,1)的比例系数，Gt为总迭代次数。当狼王发生变化时，标记消除，重新开始标记，当狼王标记累计大于等于R时，对适应度最差的种群随机重组。
 

　　GWO-PSO算法将GWO算法和PSO算法结合，使PSO算法多种群的思想引入GWO算法，通过竞争狼王而没有破坏其他灰狼结构，保证了种群的多样性与算法的寻优速度，并通过设置阈值解决了算法易陷入局部最优的问题。GWO-PSO算法的流程如图2所示。

 

       3.2算法编码与更正
 

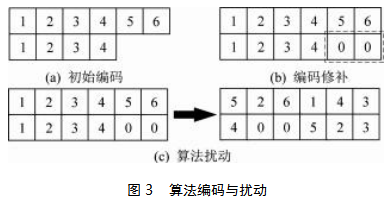
　　假设在某次任务中，包含的入库货物数量为m,出库数量为n,各项出入库任务均用自然数表示，入库任务会随机生成一个货位号。由于每批次订单出入库货物数量不相等，所以最后会形成Od项复合作业任务和Os项单一作业任务。为使算法能够循环进行，本文采用一种虚拟修补方式，使作业任务虚拟为完全复合作业，使任务编码完整。虚拟修补及算法扰动示意图如图3所示，其中，0表示补充的虚拟入库或出库任务，为描述方便，定义上排字段为入库序号，下排字段为出库序号，经过修补后的编码在算法扰动下，会进行下一步寻优。

　
 

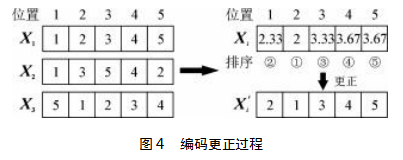
　　由于编码过程中使用整数，在利用公式(13)进行位置计算时，可能会出现某一位置向量存在小数的情况，导致算法运算错误，因此需要对带有小数的位置向量进行更正。例如：X1=[1,2,3,4,5],X2=[1,3,5,4,2],X3=[5,1,2,3,4],经过计算得Xi=[2.33,2,3.33,3.67,3.67],对Xi进行更正，将内部数字从小到大排序，当有相同小数时，按照从左到右的顺序依次排序，用序号数代替每个数字，形成新的位置向量：X=[2,1,3,4,5],具体操作如图4所示。

　　
 

　　4实例仿真与结果分析

       4.1实验参数及数据
 

　　以F配送中心为研究对象，设定自动化立体仓库共有10排15列8层，所有货格尺寸相同，堆垛机初始位置为可视为(1.5,0,1)。堆垛机面向左右两侧的货架作业，以第一台堆垛机为例，左侧货架x轴坐标始终为1,右侧货架x轴坐标始终为2。实验中，相关参数如表1所示。

　　
 

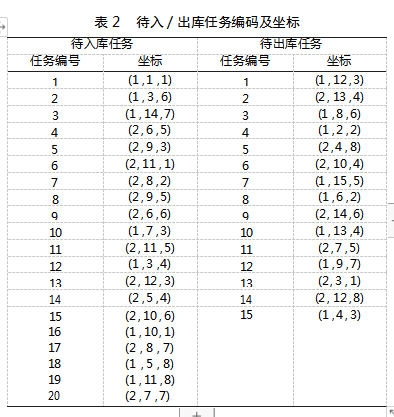
　　为验证算法在实例中的性能，为第一台堆垛机随机生成待入库和待出库任务，其中待入库任务20项，待出库任务15项，具体任务编码及坐标如表2所示。

　
 

　　4.2实例仿真验证
 

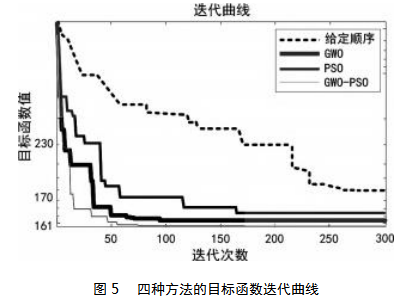
　　针对此次随机任务，分别利用给定顺序及GWO、PSO和GWO-PSO算法进行优化，迭代次数设定为300次，其迭代曲线如图5所示，给定顺序下，堆垛机单一作业任务为：待入库任务(1,1,1)、(1,3,6)、(1,14,7)、(2,6,5)、(2,9,3),三种优化算法得出的单一作业任务均为：待入库任务(1,1,1)、(1,3,6)、(2,6,5)、(1,3,4)、(2,5,4)。为方便描述，堆垛机初始位置(1.5,0,1)记为A。
 

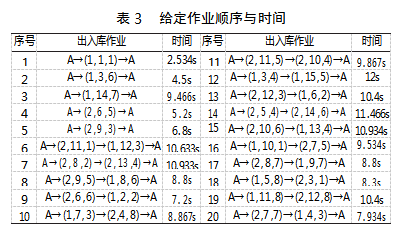
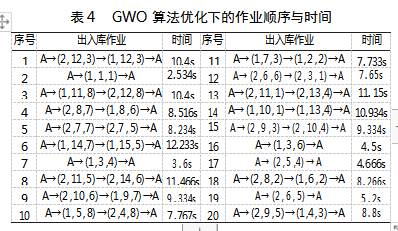
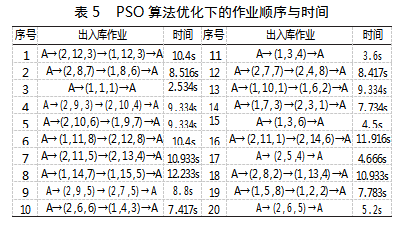
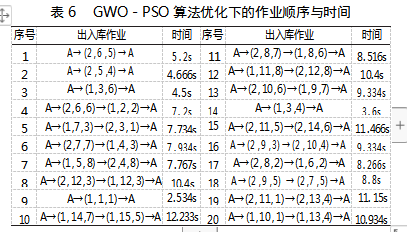
　　利用Matlab进行验证，由图5可知，PSO算法在求解本模型时收敛速度最慢，运算后期易陷入局部最优，GWO算法收敛速度适中，但全局搜索效果优于PSO算法，而GWO-PSO算法在本模型中不但有较为优秀的收敛速度，而且具有更强的全局搜索能力，各算法均缩短了堆垛机运行时间，各方法的具体作业顺序及作业时间如表3到表6所示。

 

　　给定顺序下，待出入库任务作业顺序及作业时间如表3所示，总运行时间为174.568s。

　　

　　GWO算法下，待出入库任务作业顺序及作业时间如表4所示，总运行时间为162.717s。

　
 

　　PSO算法下，待出入库任务作业顺序及作业时间如表5所示，总运行时间为163.984s。

 

　　GWO-PSO算法下，待出入库任务作业顺序及作业时间如表6所示，总运行时间为161.968s。
 

　
 

　　4.3空载优化结果
 

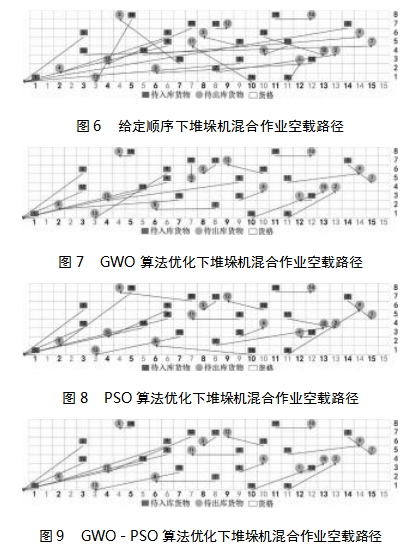
　　由于不同的作业顺序所造成的时间差最终会反映在堆垛机空载运行时间上，因此通过分析给定顺序及三种优化算法下堆垛机执行混合作业的空载时间，来分析算法的优化率，图6至图9直观展示了四种方法下的堆垛机空载路径，其中，横坐标值相同数字中，左侧数字为堆垛机左侧货位横坐标值，右侧为堆垛机右侧货位横坐标值。

　
 

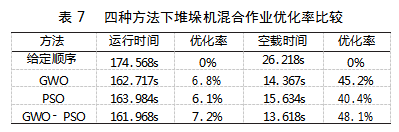
　　经过对堆垛机总体运行时间以及空载时间的分析，可以得出，GWO-PSO算法在堆垛机混合作业任务优化上均优于7.2%,空载时间优化率为48.1%,证明了GWO-PSO算法的有效性，各方法的优化比较结果如表 7 所示。

　
 

　　5结论
 

　　本文针对堆垛机混合作业模式，建立堆垛机运行时间最小的数学模型，并将GWO算法和PSO算法结合起来，形成GWO-PSO算法。首先，将灰狼个体随机分为若干群组，各群组按照标准GWO算法进行独立寻优，并推举产生首领狼王，然后采用PSO算法的位置更新方式对GWO的寻优结果进行更新，通过狼王的指导，使灰狼在位置更新时综合考虑了历史最优位置及个体最优位置，保证了种群的多样性和算法的寻优速度，接着引入速度交换算子进行离散化处理，并通过设置阈值解决了算法易陷入局部最优的问题，最后通过实例仿真分析得出，利用GWO-PSO算法求解，相比于给定顺序，堆垛于GWO算法和PSO算法的优化结果，证明了GWO-PSO算法在求解堆垛机混合作业时的有效性。