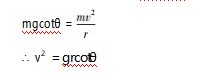SCI论文(www.lunwensci.com)
摘 要 : 通过逻辑推理,结合举出反例的方法,说明小球在光滑( 这里的“光滑”不是指没有摩 擦力的理想状况,而是指摩擦力相对很小的情形) 的魔力筒内壁运动轨迹呈螺旋形曲线下降的运
例题 如图 1 所示,该装置是某科技馆魔力 筒的示意 图,魔力筒的上下都是开口的,内表面 做抛光处理,若把小球以某一速度沿水平方向滑 入魔力筒,小球几乎可在某一水平面内运动相当 长的时 间,( 螺旋 下 降后) 最终从下面的出口滑 出,对小球在魔力筒内的运动,下列说法正确的 是( ) .
A.小球做圆周运动的周期越来越大
B.小球的向心加速度越来越大
C.小球动能越来越大
D.小球的机械能越来越大
这是早前某物理交流群一位老师给出的一道题目.给出题目的老师不清楚选项 C 是否正确,该问题在群内引起众多老师的激烈讨论,多数老师认为,小球在魔力筒内壁不断旋转运动并沿螺旋线下落过 程中,球的运动速度在不断增大,所 以 小球 的动 能越来越大,因此选项 C 正确.但持这一观 点 的 老师没有按照逻辑推理的方法说明小球速度增 大的原因,仅仅是凭自己的直观感觉——— 感觉小 球沿螺旋线在魔力筒内壁旋转并下落的过程中, 速度是在增大.那么,这一感觉正确 吗? 我们 能 否用逻辑推理的方法证明其正确性或者举出一个反例来推翻它?
该式中 g 为常量,rcotθ 是图 2 中的 BC,那么, 若小球的机械能因克服摩擦力做功而减小,其转动 的水平轨道高度降低之后,对应的 rcotθ 的值是增 大、不变还是减小呢( 这将对应于小球沿螺旋形轨 迹在魔力筒内表面旋转下落过程中,它的速度是增 大、不变还是减小,从而对应小球动能是增大、不变 还是减小) ?
先分析摩擦力在这个物理过程中对问题分析的影响.
如果小球与魔力筒的筒壁之间没有摩擦阻力, 那么,当“小球以某一速度沿水平方向滑入魔力筒” 之后,它将在筒壁内侧的某个水平面内作水平匀速 圆周运动,空间位置高度保持不变,永远不会停息下 来 ; 如果小球与魔力筒的筒壁之间存在很大的摩擦 阻力,则在魔力筒内壁滚动的小球机械能将很快减 小,在较短的时间内,小球便会下落到魔力筒下面的 出口而离开魔力筒.显然,如果小球与魔力筒内壁间的摩擦阻力足够小,我们可以保证小球在筒内壁运动任意指定长的时间,那怕是一万年——— 当然,实际 情况中摩擦力不会达到如此小的程度,我们仅仅是 通过这样的极端情形来说明相关的问题.当摩擦力 确乎这么小,小球在魔力筒内表面真的运动这么长 时间的话,尽管小球是沿筒内壁作螺旋状运动轨迹 下降的,运动过程中任何时刻的空间位置高度都比 之前任意指定时刻的空间位置高度低,但在每一圈 内的运动过程中,完全可以将小球的运动视为水平的匀速圆周运动——— 平面运动.
再分析能量损耗对解决问题的影响.
题目所给条件“魔力筒内表面作抛光处理”仅 仅是说运动的小球与筒壁间的摩擦力很小,并非没 有摩擦力,否则,小球不会沿筒壁“螺旋型下降”的, 而摩擦力越小,小球在魔力筒内运动的时间和路程 就越长,所以,整个过程中小球因克服摩擦而消耗的 机械能在小球开始具有的机械能( 以底部开口为参 考面) 中所占有的比例或许就可以很大,比如达到 50% 甚至更大,在这种情况下考虑整个过程时小球 能量的损耗显然是不可以忽略的.但是,当小球与筒 壁间的摩擦力足够小时,从小球开始进入筒壁一直 到小球从下端的出口离开筒壁的整个过程中,小球 沿魔力筒内部转动的圈数就可以任意多,比如多达 万亿圈( 我们作这样的极端假设——— 一种在理论上 可以达到的假设,依然是为了更好的说明问题,实际 的小球运动的圈数应远小于这样的天文数字) , 那么小球在一 圈或为数不多的几圈的运动过程 中,所消耗的机械能在小球开始所具有机械能中 占有的比例将非常 的小,仅为万亿分之一 ( 如果 需要的话,还可 以更小) ,显然,如此小 的 比例对 研究小球在某一 圈的运动过程中小球速度与轨 迹大小及曲面倾斜程度间关系的问题,其影响 已经降到无需考虑的地步了.
这样看来,在摩擦阻力足够 小 的情 况 下,分 析小球在某一 圈的运动过程中小球速度与魔力 筒筒壁形状之间的关系时,完全可以绕开摩擦力 和能量损耗对问题的影响,而单从“纯数学推理” 的角度( 当然需要用到运动学和动力学 的相关公式) 来进行分析.
由题目条件可知,魔力筒的内表面做抛光处理, 摩擦阻力非常的小,所以,在较短的时间或较短的路 程内,可以认为球的机械能守恒,而在长时间运动过 程中,小球的机械能因为克服摩擦力做功而不断减 小( 因此,选项 D 错误).我们不妨先分析在机械能 守恒的情况下( 比如小球在魔力筒的内表面沿筒壁 转动一周的过程中) ,小球的运动速度与曲面相关参数之间的关系.
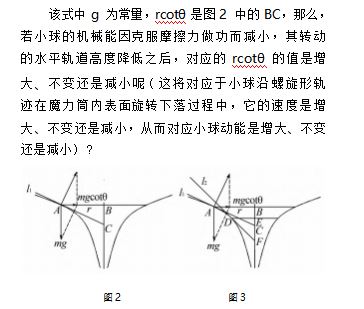
如图 2 所示,设小球以速度 v 在魔力筒内表面 作水平圆周运动时,运动轨迹半径为 r,某时刻小球 位于点 A,过小球所在点 A 作魔力筒的轴截面,设魔 力筒一侧与轴截面相交而成的曲线( 也是魔力筒曲 面的一条母线) 在 A 点的切线 l1 与竖直线的夹角为 θ , 则小球重力与曲面对小球支持力的合力( 即小球 作圆周运动的向心力) 为 mgcotθ , 则有 :
如图 3 所示,该状态是小球在魔力筒内表面运 动位置降低后的情形( 即小球在 D 点作水平 圆周 运动的情形) ,显然,这时与 rcotθ 对应的线段是图 3 中的 EF,因此,为判断小球位置降低之后速度的变化情形,只需要比较线段 EF 与 BC 的长度关系即可,当然,若能比较线段 BE 与 CF 之间长度的大小关系也可.
由图 3 可知,若中轴线两侧的曲线( 即轴截面 与魔力筒的交线) 水平向里平移的话,线段 BE 的长 度保持不变,但线段 CF 长度却要减小,只要平移的 距离足够远,肯定会出现 CF BE 的情形,具体是哪一种情 形由母线向里平移距离的长短有关).这样看来,小 球在魔力筒内表面螺旋下降的过程中,其速度可能 增大,也可能不变,还可能减小,速度的变化情形取决于魔力筒曲面的形状.
为定量分析,我们不妨以能够用数学表达式来 表示曲面母线的具体情形为例来进行分析.由于推 翻某个观点,只需举出一个反例就可以了,所以,我 们只须举出一个能够用数学表达式表示母线,并使 得小球沿内表面螺旋下降后速度减小或不变的魔力筒的例子即可.
所以,小球在魔力筒内壁作螺旋形轨迹不断下 降的运动过程中,它的动能可能增大,可能不变,也可能减小,因此上述例题选项 C 是错误的.
参考文献 :
[1] 芮宏军.数形结合方法在高中物理解题中的应用[J].数理化解题研究,2022 (7) : 88-90 .
[2]李庆国.不可忽视的中间过程——— 例析解题时 过程分析 的重要性[J].物理教 学探讨,2020 (8) : 62-64 .
[3]喻承.高中科技活动“过山车”中 的难 点与物 理原理探 究[J].物理教 学,2019 ( 5 ) : 77 -80 + 45 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/71382.html